
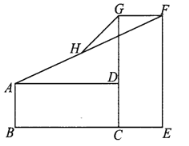
【题目】矩形![]() 与矩形
与矩形![]() 如图放置,点
如图放置,点![]() 共线,
共线,![]() 共线,连接
共线,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C. 2D.
C. 2D. ![]()
【答案】A
【解析】
如图,延长GH交AD于点M,先证明△AHM≌△FHG,从而可得AM=FG=1,HM=HG,进而得DM=AD-AM=2,继而根据勾股定理求出GM的长即可求得答案.
如图,延长GH交AD于点M,
∵四边形ABCD、CEFG是矩形,
∴AD=BC=3,CG=EF=3,FG=CE=1,∠CGF=90°,∠ADC=90°,
∴DG=CG-CD=3-1=2,∠ADG=90°=∠CGF,
∴AD//FG,
∴∠HAM=∠HFG,∠AMH=∠FGH,
又AH=FH,
∴△AHM≌△FHG,
∴AM=FG=1,HM=HG,
∴DM=AD-AM=3-1=2,
∴GM=![]() ,
,
∵GM=HM+HG,
∴GH=![]() ,
,
故选A.


科目:初中数学 来源: 题型:
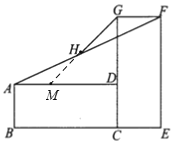
【题目】由几个相同的边长为1的小立方块搭成的几何体的俯视图如图①,格中的数字表示该位置的小立方块的个数.
(1)请在下面方格纸图②中分别画出这个几何体的主视图和左视图.
(2)根据三视图,这个组合几何体的表面积为多少个平方单位?(包括底面积)
(3)若上述小立方块搭成的几何体的俯视图不变,如图③,各位置的小立方块个数可以改变(总数目不变),则搭成这样的组合几何体中的表面积最大(包括底面积)仿照图①,将数字填写在图③的正方形中.
查看答案和解析>>
科目:初中数学 来源: 题型:
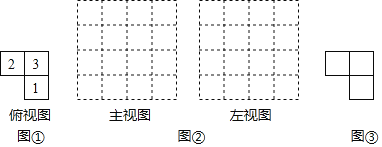
【题目】如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
A. ∠A=∠C B. AD∥BC C. BE=DF D. AD=CB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情景:如图1,在等腰直角三角形ABC中∠ACB=90°,BC=a.将AB绕点B顺时针旋转90°得到线段BD,连接CD,过点D作△BCD的BC边上的高DE.
易证△ABC≌△BDE,从而得到△BCD的面积为![]() .
.
简单应用:如图2,在Rt△ABC中,∠ACB=90°,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,用含a的代数式表示△BCD的面积,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
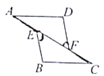
【题目】如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.
(1)求证:△ABC≌△DEF;
(2)求证:四边形ACFD为平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 在平面直角坐标系中,
在平面直角坐标系中, ![]() ,
,![]() ,把矩形
,把矩形![]() 沿直线
沿直线![]() 对折使点
对折使点![]() 落在点
落在点![]() 处,直线
处,直线![]() 与
与![]() 的交点分别为
的交点分别为![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在坐标平面内,若四边形
在坐标平面内,若四边形![]() 是菱形,则菱形
是菱形,则菱形![]() 的面积是( )
的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com