【题目】将一元二次方程x2﹣2x﹣3=0配方后所得的方程是（ ）
A. （x﹣2）2=4 B. （x﹣1）2=4 C. （x﹣1）2=3 D. （x﹣2）2=3
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】在研究圆的有关性质时，我们曾做过这样的一个操作“将一张圆形纸片沿着它的任意一条直径翻折，可以看到直径两侧的两个半圆互相重合”．由此说明（ ）
A. 圆是中心对称图形，圆心是它的对称中心
B. 圆是轴对称图形，任意一条直径所在的直线都是它的对称轴
C. 圆的直径互相平分
D. 垂直弦的直径平分弦及弦所对的弧
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，EF∥AD,∠1=∠2,∠B=35°,将求∠BDG的过程填写完整。
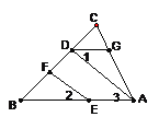
解： ∵EF∥AD，
∴∠2=____ (________________________________)
又∵∠1=∠2
∴∠1= ( 等量代换 )
∴DG∥_____ (___________________________________)
∴∠B+______=180°(___________________________)
∵∠B=35°
∴∠BDG =_______
查看答案和解析>>
科目：初中数学 来源： 题型：
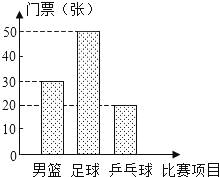
【题目】下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格，某公司购买的门票种类、数量绘制的条形统计图如图．
比赛项目 | 票价（元/张） |
男 篮 | 1000 |
足 球 | 800 |
乒乓球 | x |
依据上列图、表，回答下列问题：
（1）其中观看男篮比赛的门票有 张；观看乒乓球比赛的门票占全部门票的 %；
（2）公司决定采用随机抽取的方式把门票分配给100名员工，在看不到门票的条件下，每人抽取一张（假设所有的门票形状、大小、质地等完全相同且充分洗匀），问员工小亮抽到足球门票的概率是 ；
（3）若购买乒乓球门票的总款数占全部门票总款数的
，试求每张乒乓球门票的价格．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①、②、③中，点E、D分别是正△ABC、正四边形ABCM、正五边形ABCMN中以C点为顶点的相邻两边上的点，且BE=CD，DB交AE于P点．
（1）分别求图①，图②和图③中，∠APD的度数.
（2）根据前面探索，你能否将本题推广到一般的正n边形情况？若能，写出推广问题和结论；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】倡导研究性学习方式，着力教材研究，习题研究，是学生跳出题海，提高学习能力和创新能力的有效途径．下面是一案例，请同学们认真阅读、研究，完成“类比猜想”及后面的问题．
习题解答
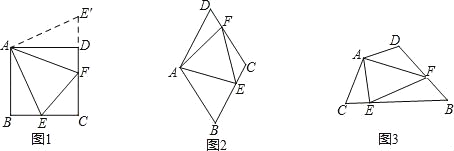
习题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，说明理由．
解：
∵正方形ABCD中，AB=AD，∠BAD=∠ADC=90°
∴把△ABE绕点A逆时针旋转90°至△ADE′，点F、D、E′在一条直线上．
∴∠E′AF=90°-45°=45°=∠EAF．
又∵AE′=AE，AF=AF
∴△AE′FF≌△AEF（SAS）
∴EF=E′F=DE′+DF=BE+DF．
习题研究．
观察分析：
观察图1，由解答可知，该题有用的条件是①．ABCD是四边形，点E、F分别在边BC、CD上；②．AB=AD；③．∠B=∠D=90°∠；④．∠EAF=
∠BAD．
类比猜想：
在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD，∠B=∠D时，还有EF=BE+DF吗？
要解决上述问题，可从特例入手，请同学们思考：如图2，在菱形ABCD中，点E、F分别在BC、CD上，当∠BAD=120°，∠EAF=60°时，还有EF=BE+DF吗？试证明．
（2）在四边形ABCD中，点E、F分别在边BC、CD上，当AB=AD，∠B+∠D=180°，∠EAF=
∠BAD时，还有EF=BE+DF吗？使用图3证明．
归纳概括：
反思前面的解答，思考每个条件的作用，可以得到一个结论“EF=BE+DF”的一般命题： ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
