
分析 (1)根据点的坐标利用待定系数法即可求出一次函数的表达式,再标上x的取值范围即可;
(2)根据y<2即可得出关于x的一元一次不等式,解之即可得出结论;
(3)根据一次函数图象上点的坐标特征即可求出y1、y2的值,比较后即可得出结论.
解答 解:(1)设一次函数的表达式为y=kx+b(k≠0),
将(1,1)、(-2,7)代入y=kx+b,
$\left\{\begin{array}{l}{k+b=1}\\{-2k+b=7}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-2}\\{b=3}\end{array}\right.$,
∴一次函数的表达式为y=-2x+3(x∈R).
(2)当y<2时,有-2x+3<2,
解得:x>$\frac{1}{2}$,
∴当y<2时,自变量x的取值范围为x>$\frac{1}{2}$.
(3)∵x1=m,x2=m+1,
∴y1=-2m+3,y2=-2m+1.
∵-2m+3>-2m+1,
∴y1>y2.
点评 本题考查了待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,解题的关键是:(1)根据点的坐标利用待定系数法求出函数关系式;(2)根据y的范围找出关于x的一元一次不等式;(3)根据一次函数图象上点的坐标特征求出y1、y2的值.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
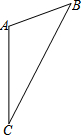 按要求作图,不必写作图过程,但必须保留作图痕迹.
按要求作图,不必写作图过程,但必须保留作图痕迹.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -|-2|=2 | B. | (6.4×106)÷(8×103)=800 | ||
| C. | (-1)2015-12016=-2 | D. | $-6÷({\frac{1}{3}-\frac{1}{2}})=36$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
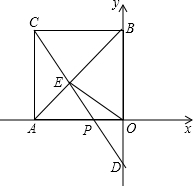 在平面直角坐标系xOy中,四边形OACB是正方形,A点的坐标为(-3,0),点P是射线AO上(异于点A、O)一动点,直线CP与对角线AB及y轴分别交于点E,D.
在平面直角坐标系xOy中,四边形OACB是正方形,A点的坐标为(-3,0),点P是射线AO上(异于点A、O)一动点,直线CP与对角线AB及y轴分别交于点E,D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com