练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    在一个广场上有两棵树，一棵高6米，另一棵高2米，两树相距5米．一只小鸟从一棵树的树梢飞到另一棵树的树梢，至少飞了       米.
    本题主要考查了勾股定理的应用
    根据“两点之间线段最短”可知：小鸟沿着两棵树的树尖进行直线飞行，所行的路程最短，运用勾股定理可将两点之间的距离求出．
    两棵树的高度差为6-2=4m，间距为5m，
    根据勾股定理可得：小鸟至少飞行的距离
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：填空题

    Rt△ABC中，若∠C＝90°，sinA=，AB=10，则BC=        ．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    计算：

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    如图（1）、（2）中，（1）正方形A的面积为             .（2）斜边x=             .

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    如图，分别以△ABC的三边为边向外作3个正方形，面积分别为1，2，3，则此△ABC________(填“是”，“不是”) 直角三角形．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    下列各组数中以a，b，c为边的三角形不是Rt△的是（　 　）
    A．a=2，b=3，c=4B．a=7，b=24，c=25C．a=6，b=8，c=10D．a=3，b=4，c=5

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    三角形的三边长分别为6、8、10，它的最短边上的高为(     )
    A．6B．4.5C．2.4D．8

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

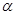    如图，点O是等边△ABC内一点，∠AOB=110º，∠BOC=,将△BOC绕点C按顺时针方向旋转60º得△ADC，连接OD．
    （1）△COD是什么三角形？说明理由；
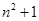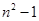    （2）若AO=，AD=,OD=(为大于1的整数)，求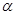的度数；
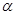    （3）当为多少度时，△AOD是等腰三角形？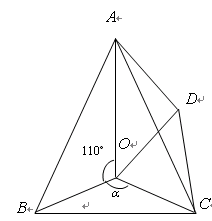

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

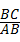    通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做顶角正对（sad），如图①，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sadA=底边/腰=．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．根据上述角的正对定义，解下列问题：
    （1）sad60°=　    　．
    （2）对于0°＜A＜180°，∠A的正对值sadA的取值范围是　       　．
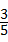    （3）如图②，已知sinA=，其中∠A为锐角，试求sadA的值．

    查看答案和解析>>

    同步练习册答案