
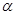 ,将△BOC绕点C按顺时针方向旋转60º得△ADC,连接OD.
,将△BOC绕点C按顺时针方向旋转60º得△ADC,连接OD.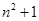 ,AD=
,AD=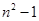 ,OD=
,OD= (
( 为大于1的整数),求
为大于1的整数),求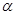 的度数;
的度数; 为多少度时,△AOD是等腰三角形?
为多少度时,△AOD是等腰三角形? 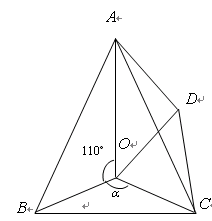
 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的三个顶点均在格点上,请按要求完成下列各题:
的三个顶点均在格点上,请按要求完成下列各题: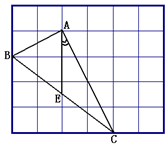
 的三个内角中任选一个锐角,若你所选的锐角是 ,则它所对应的正弦函数值是 .
的三个内角中任选一个锐角,若你所选的锐角是 ,则它所对应的正弦函数值是 .查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com