
【题目】如图,在平面直角坐标系xOy中,一次函数y1=kx+b的图象与反比例函数y2=![]() 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.

(1)求一次函数和反比例函数的解析式;
(2)请直接写出,当x取何值时,y1>y2?
(3)若P是y轴上一点,且满足△PAB的面积是5,请直接写出OP的长.
【答案】(1)y2=![]() ,y1=x+1;(2)-3<x<0或x>2;(3)OP=3或OP=1
,y1=x+1;(2)-3<x<0或x>2;(3)OP=3或OP=1
【解析】
(1)将A坐标代入反比例函数解析式中求出m的值,即可确定出反比例函数解析式;将B坐标代入反比例解析式中求出n的值,确定出B坐标,将A与B坐标代入一次函数解析式中求出k与b的值,即可确定出一次函数解析式;
(2)根据图象即可得出不等式y1>y2的解集
(3)如图所示,对于一次函数解析式,令x=0求出y的值,确定出C坐标,得到OC的长,三角形ABP面积由三角形ACP面积与三角形BCP面积之和求出,由已知的面积求出PC的长,即可求出OP的长.
(1)∵A(2,3),B(-3,n)在反比例函数y2=![]() 的图象上,
的图象上,
∴ ,解得
,解得![]()
∴反比例函数的解析式为y2=![]() ,
,
∴B(-3,-2) .
∵A(2,3),B(-3,-2)在一次函数y1=kx+b的图象上,
∴![]() 解得,
解得,![]()
∴一次函数的解析式为y1=x+1.
(2)观察函数图象可知:当-3<x<0或x>2时,y1>y2;
(3) 对于一次函数y=x+1,令x=0求出y=1,即C(0,1),OC=1,
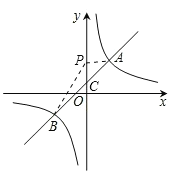
根据题意得:S△ABP=![]() PC×2+
PC×2+![]() PC×3=5,
PC×3=5,
解得:PC=2,
则OP=OC+CP=1+2=3或OP=CP-OC=2-1=1.
故OP的长是3或1.


科目:初中数学 来源: 题型:
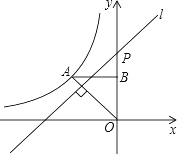
【题目】如图,反比例函数y=![]() (x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是________.
(x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,连接
的中点,连接![]() .将
.将![]() 绕点
绕点![]() 顺时针方向旋转,记旋转角为
顺时针方向旋转,记旋转角为![]() .
.
①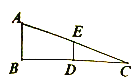 ②
②
③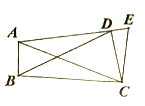 ④
④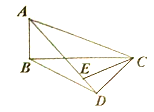
(1)问题发现:当![]() 时,
时,![]() .
.
(2)拓展探究:试判断:当![]() 时,
时,![]() 的大小有无变化?请仅就图②的情况给出证明.
的大小有无变化?请仅就图②的情况给出证明.
(3)问题解决:当![]() 旋转至
旋转至![]() 三点共线时,如图③,图④,直接写出线段
三点共线时,如图③,图④,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
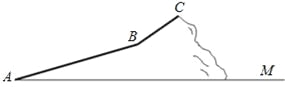
【题目】今年“五一“假期.某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点.再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为30°.已知A点海拔121米.C点海拔721米.
(1)求B点的海拔;
(2)求斜坡AB的坡度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某建筑物,从10m高的窗口A,用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面![]() m,则水流落地点B离墙的距离OB是( )
m,则水流落地点B离墙的距离OB是( )
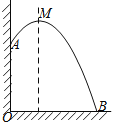
A.2mB.3mC.4mD.5m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位在疫情期间用3000元购进A、B两种口罩1100个,购买A种口罩与购买B种口罩的费用相同,且A种口罩的单价是B种口罩单价的1.2倍;
(1)求A,B两种口罩的单价各是多少元?
(2)若计划用不超过7000元的资金再次购进A、B两种口罩共2600个,已知A、B两种口罩的进价不变,求A种口罩最多能购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
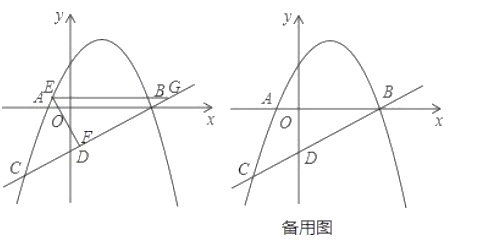
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() 为二次函数图象上任一点.
为二次函数图象上任一点.
![]() 求这个二次函数的解析式;
求这个二次函数的解析式;
![]() 若点
若点![]() 是直线
是直线![]() 上方抛物线上一点,过
上方抛物线上一点,过![]() 分别作
分别作![]() 和
和![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于不同的两点
于不同的两点![]() 在
在![]() 的左侧),求
的左侧),求![]() 周长的最大值;
周长的最大值;
![]() 是否存在点
是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角边的直角三角形?如果存在,求点
为直角边的直角三角形?如果存在,求点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3经过点A (1,0)和点B (-3,0),与y轴交于点C,点P为第二象限内抛物线上的动点.
(1)抛物线的解析式为__________,抛物线的项点坐标为__________;
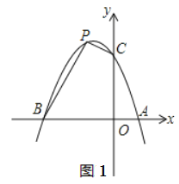
(2)如图1,是否存在点P,使四边形BOCP的面积为8?若存在,请求出点P的坐标;若不存在,请说明理由.
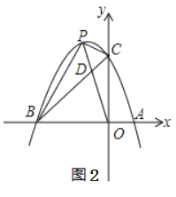
(3)如图2,连接OP交BC于点D,当S△CPD∶S△BPD=1∶2时,请求出点D的坐标;
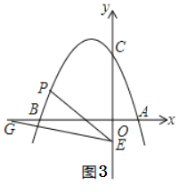
(4)如图3,点E的坐标为(0,-1),点G为x轴负半轴上的一点,∠OGE=15°,连接PE,若∠PEG=2∠OGE,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
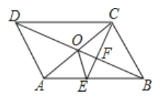
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边的中点,将
边的中点,将![]() 绕
绕![]() 点旋转
点旋转![]() 得到
得到![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有______(只填写序号).
.其中正确的结论有______(只填写序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com