
����Ŀ��ijˮ������������ÿ�����Ϊ40Ԫ�ĸ��٣���۲��Ź涨ÿ���ۼ۲��ø���55Ԫ���г����鷢�֣���ÿ����45Ԫ�ļ۸����ۣ�ƽ��ÿ������105�䣻ÿ����50Ԫ�ļ۸����ۣ�ƽ��ÿ������90�䣮�ٶ�ÿ��������y���䣩�����ۼ�x��Ԫ/�䣩֮������һ�κ�����ϵʽ��
��1����ƽ��ÿ��������y���䣩�����ۼ�x��Ԫ/�䣩֮��ĺ�����ϵʽ��
��2�����������ƽ��ÿ�����������w��Ԫ�������ۼ�x��Ԫ/�䣩֮��ĺ�����ϵʽ��
��3����ÿ��ƻ�������ۼ�Ϊ����Ԫʱ�����Ի�����������������Ƕ��٣�
���𰸡�(1)��y����3x��240;��2��w����3 x2��360x��9600;��3�� ��ÿ��ƻ�������ۼ�Ϊ55Ԫʱ�����Ի���������Ϊ1125Ԫ.
��������
��1������ÿ��������y���䣩�����ۼ�x��Ԫ/�䣩֮������һ�κ�����ϵʽ�����ô���ϵ�������һ�κ�������ʽ���ɣ�
��2�����ø�������ƽ��ÿ�����������w��Ԫ��=ÿ�������������ÿ����������ó����ɣ�
��3�����������������Ա�����ȡֵ�õ����ε���ֵ���⼴�ɣ�
��1����y=kx+b��
����֪��45��105������50��90������ã�
![]() ��
��
��ã�![]() ��
��
��ƽ��ÿ��������y���䣩�����ۼ�x��Ԫ/�䣩֮��ĺ�����ϵʽΪ��y=-3x+240��
��2����ˮ������������ÿ�����Ϊ40Ԫ��ƻ�������ۼ�xԪ/�䣬
���������ƽ��ÿ�����������w��Ԫ�������ۼ�x��Ԫ/�䣩֮��ĺ�����ϵʽΪ��
W=��x-40����-3x+240��=-3x2+360x-9600��
��3��W=-3x2+360x-9600=-3��x-60��2+1200��
��a=-3��0���������߿������£�
�֡߶Գ���Ϊx=60���൱x��60��W��x�����������
����50��x��55���൱x=55ʱ��W�����ֵΪ1125Ԫ��
�൱ÿ��ƻ�������ۼ�Ϊ55Ԫʱ�����Ի���������Ϊ1125Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij����D�����ɽ��C������Ϊ37������ǰ��100������ɽ��A�������ɽ��AC���¶�Ϊi=1��0.5����ɽ�ĸ߶ȣ����Ʋ���ǵĸ߶ȣ��ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCDΪ�����Σ���EΪ�߶�AC��һ�㣬����DE������E��EF��DE��������BC�ڵ�F����DE��EFΪ�ڱ�������DEFG������CG��
��1����ͼ1����֤������DEFG�������Σ�
��2����AB=2��CE=![]() ����CG�ij��ȣ�
����CG�ij��ȣ�
��3�����߶�DE��������ABCD��ij���ߵļн���30��ʱ��ֱ��д����EFC�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
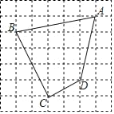
����Ŀ����ͼ��ÿ��С�����εı߳���Ϊ1���ı���ABCD�Ķ��㶼��С�����εĶ����ϣ�
��1�����ı���ABCD�������
��2����BCD��ֱ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���֪��A��a��a����B��a��a��3��������aΪ��������C���߶�AB�ϣ��ҵ�C�ĺ��������Ϊ������
��1����a��1ʱ�������߶�AB��
��2������C��x���ϣ������C�����ꣻ
��3������C����������![]() ��ֱ��д��a�����п���ȡֵ���� ����
��ֱ��д��a�����п���ȡֵ���� ����
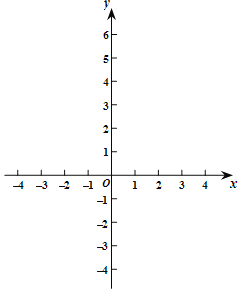
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ũ��ʦʯ������ij��ѧ������1�����ѧ������һ����ѧ����У������������㳡�����������ڹ㳡���ĵ�������ͭ��߶ȣ���֪ͭ������ĸ�Ϊ3.5m��ijС���ʵϰ������������������ͭ��ĸߣ������ȷ��0.1m��
ʵϰ����2003��9��25��
��Ŀ1 | �����ײ����Ե����ͭ��� | |||
| ||||
�� �� �� �� | ������Ŀ | ��һ�� | �ڶ��� | ƽ��ֵ |
BD�ij� | 12.3m | 11.7m | ||
������CD�ĸ� | 1.32m | 1.28m | ||
��� | ��=30��56' | ��=31��4' | ||
�� �� | ||||
��� | ||||
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC �У�AB=AC����C=70�㣬��AB��C������ABC ����ֱ�� EF�Գƣ���CAF=10�㣬���� BB�������ABB���Ķ����ǣ� ��

A. 30�� B. 35�� C. 40�� D. 45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ֧Ԯ��ɽ����ijѧУ���ĻС�����óO���ʽ���A��B�����ͺŵ�ѧϰ��Ʒ����֪B��ѧϰ��Ʒ�ĵ��۱�A��ѧϰ��Ʒ�ĵ��۶�10Ԫ����180Ԫ����B��ѧϰ��Ʒ����120Ԫ����A��ѧϰ��Ʒ�ļ�����ͬ��
��1����A��B����ѧϰ��Ʒ�ĵ��۸��Ƕ���Ԫ��
��2��������A��B����ѧϰ��Ʒ��1000�������ܷ��ò�����28000Ԫ��������B��ѧϰ��Ʒ���ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
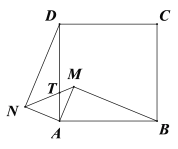
����Ŀ����ͼ����Rt��ABM��Rt��ADN��б�߷ֱ�Ϊ�����εı�AB��AD������AM=AN.
(1)��֤��Rt��ABM��Rt��AND
(2)�߶�MN���߶�AD�ཻ��T����AT=![]() ,��
,��![]() ��ֵ
��ֵ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com