
【题目】如图,直线y=﹣x+5与双曲线![]() (x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是
(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是![]() .若将直线y=﹣x+5向下平移1个单位,则所得直线与双曲线
.若将直线y=﹣x+5向下平移1个单位,则所得直线与双曲线![]() (x>0)的交点有( )
(x>0)的交点有( )
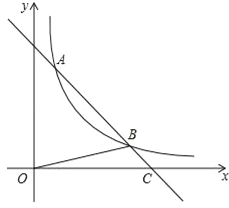
A.0个 B.1个 C.2个 D.0个,或1个,或2个
【答案】B.
【解析】
试题分析:令直线y=﹣x+5与y轴的交点为点D,过点O作OE⊥直线AC于点E,过点B作BF⊥x轴于点F,如图所示.
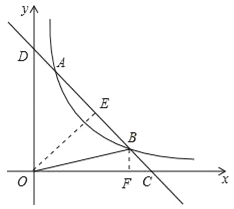
令直线y=﹣x+5中x=0,则y=5,即OD=5;
令直线y=﹣x+5中y=0,则0=﹣x+5,解得:x=5,即OC=5.
在Rt△COD中,∠COD=90°,OD=OC=5,∴tan∠DCO=![]() =1,∠DCO=45°.
=1,∠DCO=45°.
∵OE⊥AC,BF⊥x轴,∠DCO=45°,∴△OEC与△BFC都是等腰直角三角形,又∵OC=5,∴OE=![]() .∵S△BOC=
.∵S△BOC=![]() BCOE=
BCOE=![]() BC=
BC=![]() ,∴BC=
,∴BC=![]() ,∴BF=FC=
,∴BF=FC=![]() BC=1,∵OF=OC﹣FC=5﹣1=4,BF=1,∴点B的坐标为(4,1),∴k=4×1=4,即双曲线解析式为
BC=1,∵OF=OC﹣FC=5﹣1=4,BF=1,∴点B的坐标为(4,1),∴k=4×1=4,即双曲线解析式为![]() .
.
将直线y=﹣x+5向下平移1个单位得到的直线的解析式为y=﹣x+5﹣1=﹣x+4,将y=﹣x+4代入到![]() 中,得:
中,得:![]() ,整理得:
,整理得:![]() ,∵△=16﹣4×4=0,∴平移后的直线与双曲线
,∵△=16﹣4×4=0,∴平移后的直线与双曲线![]() 只有一个交点.故选B.
只有一个交点.故选B.


科目:初中数学 来源: 题型:
【题目】某小区2015年屋顶绿化面积为2000平方米,计划2017年屋顶绿化面积要达到2880平方米.若设屋顶绿化面积的年平均增长率为x,则依题意所列方程正确的是( )
A. 2000x2=2880 B. 2000(1+2x)=2880
C. 2000(1+x)2=2880 D. 2000(1﹣x)2=2880
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,BE平分∠ABC,CF平分∠BCD,BE、CF交于点G.若使EF=![]() AD,那么平行四边形ABCD应满足的条件是( )
AD,那么平行四边形ABCD应满足的条件是( )

A. ∠ABC=60° B. AB:BC=1:4 C. AB:BC=5:2 D. AB:BC=5:8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.
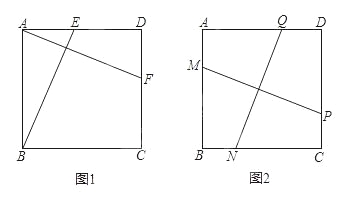
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别是(﹣3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.

(1)当点C运动到线段OB的中点时,求t的值及点E的坐标;
(2)当点C在线段OB上时,求证:四边形ADEC为平行四边形;
(3)在线段PE上取点F,使PF=2,过点F作MN⊥PE,截取FM=![]() ,FN=1,且点M,N分别在第一、四象限,在运动过程中,当点M,N中,有一点落在四边形ADEC的边上时,直接写出所有满足条件的t的值.
,FN=1,且点M,N分别在第一、四象限,在运动过程中,当点M,N中,有一点落在四边形ADEC的边上时,直接写出所有满足条件的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上的动点,点
上的动点,点![]() 是射线
是射线![]() 上一点,射线
上一点,射线![]() 和射线
和射线![]() 交于点
交于点![]() ,且
,且![]() .
.

(1)求线段![]() 的长;
的长;
(2)如果![]() 是以
是以![]() 为腰的等腰三角形,求线段
为腰的等腰三角形,求线段![]() 的长;
的长;
(3)如果点![]() 在边
在边![]() 上(不与点
上(不与点![]() 、
、![]() 重合),设
重合),设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com