
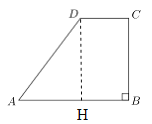
【题目】如图所示,梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上的动点,点
上的动点,点![]() 是射线
是射线![]() 上一点,射线
上一点,射线![]() 和射线
和射线![]() 交于点
交于点![]() ,且
,且![]() .
.

(1)求线段![]() 的长;
的长;
(2)如果![]() 是以
是以![]() 为腰的等腰三角形,求线段
为腰的等腰三角形,求线段![]() 的长;
的长;
(3)如果点![]() 在边
在边![]() 上(不与点
上(不与点![]() 、
、![]() 重合),设
重合),设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
【答案】(1)7;(2)15或![]() ;(3)
;(3)![]() (
(![]() ).
).
【解析】
试题分析:(1)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,由勾股定理求出AH的长,进而求出DC的长;
,由勾股定理求出AH的长,进而求出DC的长;
(2)可证![]() ∽
∽![]() ,从而得到
,从而得到![]() 是以
是以![]() 为腰的等腰三角形,分两种情况讨论:① 若
为腰的等腰三角形,分两种情况讨论:① 若![]() ,② 若
,② 若![]() ;
;
(3)表示出DE的长,由![]() ∽
∽![]() ,得出EG的长,从而得出DG的长,由DF∥AE,得到
,得出EG的长,从而得出DG的长,由DF∥AE,得到![]() ,化简即可得到结论.
,化简即可得到结论.
试题解析:(1)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .在Rt
.在Rt![]() 中,
中,![]() ,
,![]() ,
,![]() ,∴
,∴![]() .又∵
.又∵![]() ,∴
,∴![]() ;
;
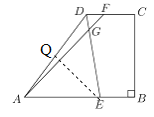
(2)∵![]() ,又
,又![]() ,∴
,∴![]() ∽
∽![]() .由
.由![]() 是以
是以![]() 为腰的等腰三角形,可得
为腰的等腰三角形,可得![]() 是以
是以![]() 为腰的等腰三角形.
为腰的等腰三角形.
① 若![]() ,∵
,∵![]() ,∴
,∴![]() ;
;
② 若![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,∴
,∴![]() .
.
在Rt![]() 中,
中,![]() ,
,![]() ;
;
在Rt![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() ;
;
综上所述:当![]() 是以
是以![]() 为腰的等腰三角形时,线段
为腰的等腰三角形时,线段![]() 的长为15或
的长为15或![]() ;
;
(3)在Rt![]() 中,
中,![]() ,
,![]() .∵
.∵![]() ∽
∽![]() ,∴
,∴![]() ,∴
,∴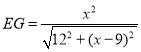 ,∴
,∴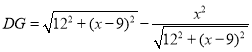 .∵
.∵![]() ∥
∥![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,
,![]() 的取值范围为
的取值范围为![]() .
.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+5与双曲线![]() (x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是
(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是![]() .若将直线y=﹣x+5向下平移1个单位,则所得直线与双曲线
.若将直线y=﹣x+5向下平移1个单位,则所得直线与双曲线![]() (x>0)的交点有( )
(x>0)的交点有( )
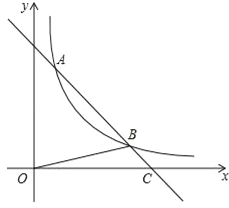
A.0个 B.1个 C.2个 D.0个,或1个,或2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P从原点O出发,每次向上平移2个单位长度或向右平移1个单位长度.
(1)实验操作:
在平面直角坐标系中描出点P从点O出发,平移1次后,2次后,3次后可能到达的点,并把相应点的坐标填写在表格中:
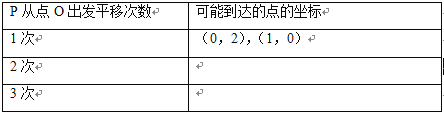
(2)观察发现:
设点P(x,y),任一次平移,点P可能到达的点的纵、横坐标都满足一定的关系式.
例如:平移1次后2x+y= _________;平移2次后2x+y= ;平移3次后2x+y= ;……由此我们知道,平移n次后点P的坐标都满足一定的关系式是 ;
(3)探索运用:
点P从点O出发经过n次平移后到达点Q,若点Q的纵坐标比横坐标大6,并且P平移的路径长不小于50,不超过56,请直接写出Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
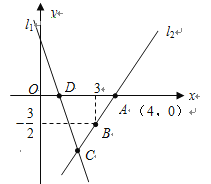
【题目】如图,直线![]() 的解析式为
的解析式为![]() ,且
,且![]() 与
与![]() 轴交于点D,直线
轴交于点D,直线![]() 经过点
经过点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 交于点C.
交于点C.
(1)求直线![]() 的解析表达式;
的解析表达式;
(2)求![]() 的面积;
的面积;
(3)在直线![]() 上存在异于点C的另一点P,使得
上存在异于点C的另一点P,使得![]() 与
与![]() 的面积相等,请求出点P的坐标.
的面积相等,请求出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com