
 交x轴于点E、C(点C在点E的右侧),交y轴于点A,它的对称轴过点D,顶点为点F;
交x轴于点E、C(点C在点E的右侧),交y轴于点A,它的对称轴过点D,顶点为点F;
 (x-2)(x-6)中,令y=0,得 x1=2、x2=6;
(x-2)(x-6)中,令y=0,得 x1=2、x2=6; ;
; )、E(2,0)、C(6,0);
)、E(2,0)、C(6,0); );
); (2)在Rt△ABO中,OA=2
(2)在Rt△ABO中,OA=2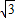 ,OB=2,那么 tan∠ABO=
,OB=2,那么 tan∠ABO= =
= =
=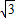 ,∠ABO=60°;
,∠ABO=60°; ∠ABO=30°,交y轴于点H,则H(0,
∠ABO=30°,交y轴于点H,则H(0, ),
), x+
x+ ;
; ,解得
,解得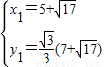 ,
,
 ,
, )、(5-
)、(5- ,
, ).
). (3)由(1)的抛物线解析式可得:F(4,-
(3)由(1)的抛物线解析式可得:F(4,- );
);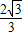 ,CG=2,所以tan∠FCG=
,CG=2,所以tan∠FCG= =
=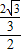 =
= ,即∠FCG=30°;
,即∠FCG=30°; EC=2,DR=CD-CR=4-2=2;
EC=2,DR=CD-CR=4-2=2;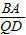 =
=
 =
= ,化简,得:t2-4t+8=0
,化简,得:t2-4t+8=0

 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
| ||
| 6 |

查看答案和解析>>
科目:初中数学 来源: 题型:
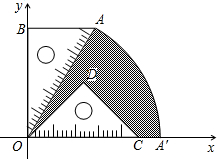 ODC的斜边OC的长相等,把这两块三角板放置在如图所示的平面直角坐标系中,且AB=3,AO=6.
ODC的斜边OC的长相等,把这两块三角板放置在如图所示的平面直角坐标系中,且AB=3,AO=6.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
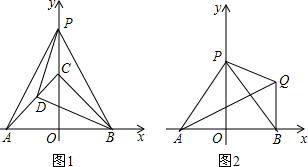 D为AC的中点.
D为AC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com