
【题目】在平面直角坐标系中,抛物线y=﹣![]() x2+
x2+![]() x+4的图象与x轴交于B,C两点(B在C的左侧),与y轴交于点A.
x+4的图象与x轴交于B,C两点(B在C的左侧),与y轴交于点A.
(1)求出点A,B,C的坐标.
(2)在抛物线上有一动点P,抛物线的对称轴上有另一动点Q,若以B,C,P,Q为顶点的四边形是平行四边形,直接写出点P的坐标.
(3)向右平移抛物线,使平移后的抛物线恰好经过△ABC的外心,求出平移后的抛物线的解析式.
【答案】(1)A(0,4),B(﹣2,0),C(8,0);(2)P(3,![]() )或(﹣7,﹣
)或(﹣7,﹣![]() )或(13,﹣
)或(13,﹣![]() );(3)y=﹣
);(3)y=﹣![]() +4x﹣
+4x﹣![]()
【解析】
(1)分别令x=0和y=0代入可求得点A,B,C的坐标;
(2)利用配方法求出抛物线的顶点坐标,分三种情况:当P在x轴的上方时,即为抛物线的顶点P(3,![]() );当P在x轴的下方时,有两种情况:①当P在抛物线对称轴的左侧时,如图2,②当P在抛物线对称轴的右侧时,如图3,根据PQ=BC=10,求出横坐标后再求纵坐标;
);当P在x轴的下方时,有两种情况:①当P在抛物线对称轴的左侧时,如图2,②当P在抛物线对称轴的右侧时,如图3,根据PQ=BC=10,求出横坐标后再求纵坐标;
(3)通过证明△AOB∽△COA,得△ABC是直角三角形,得△ABC的外心E的坐标为(3,0),则抛物线向右平移5个单位,由此写出平移后的抛物线的解析式.
解:(1)当x=0时,y=4,
∴与y轴交点A(0,4),
当y=0时,﹣![]() x2+
x2+![]() x+4=0,
x+4=0,
解得:x=﹣2或8,
∴B(﹣2,0),C(8,0);
(2)y=﹣![]() x2+
x2+![]() x+4=﹣
x+4=﹣![]() (x﹣3)2+
(x﹣3)2+![]() ,
,
当P在x轴的上方时,即为抛物线的顶点P(3,![]() )时,可以构成平行四边形BPCQ,如图1,
)时,可以构成平行四边形BPCQ,如图1,
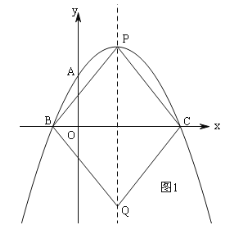
当P在x轴的下方时,
∵BC=2+8=10,
若四边形BPCQ为平行四边形,则BC∥PQ,BC=PQ=10,
有两种情况:①当P在抛物线对称轴的左侧时,如图2,
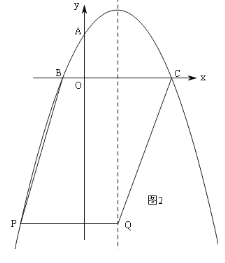
∴点P的横坐标为﹣7,
当x=﹣7时,y=﹣![]() ×(﹣7)2+
×(﹣7)2+![]() ×(﹣7)+4=﹣
×(﹣7)+4=﹣![]() ,
,
此时P(﹣7,﹣![]() );
);
②当P在抛物线对称轴的右侧时,如图3,
∴点P的横坐标为13,
当x=13时,y=﹣![]() ×132+
×132+![]() ×13+4=﹣
×13+4=﹣![]() ,
,
此时P(13,﹣![]() );
);
综上所述,点P的坐标为P(3,![]() )或(﹣7,﹣
)或(﹣7,﹣![]() )或(13,﹣
)或(13,﹣![]() );
);
(3)如图3,
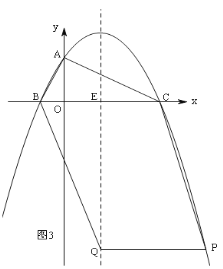
∵A(0,4)、B(﹣2,0)、C(8,0)
∴OA=4,OB=2,OC=8,
∴![]()
∴![]() ,
,
∵∠AOB=∠AOC=90°,
∴△AOB∽△COA,
∴∠BAO=∠ACO,
∵∠ACO+∠OAC=90°,
∴∠BAO+∠OAC=90°,
∴∠BAC=90°,
∴△ABC是直角三角形,
∴△ABC的外心就是斜边BC的中点E,
∵BC=10,
∴BC的中点E的坐标为(3,0),
即平移后的解析式经过E(3,0),
∴相当于把原抛物线向右平移5个单位,
∴平移后的解析式为:y=﹣![]() (x﹣3﹣5)2+
(x﹣3﹣5)2+![]() =﹣
=﹣![]() +4x﹣
+4x﹣![]() .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】如图,把一张边长为10cm的正方形纸板的四周各剪去一个边长为xcm的小正方形,再折叠成一个无盖的长方体盒子.
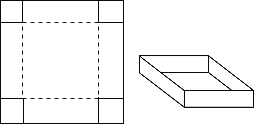
(1)当长方体盒子的底面积为81cm2时,求所剪去的小正方形的边长.
(2)设所折叠的长方体盒子的侧面积为S,求S与x的函数关系式,并写出x的取值范围.
(3)长方体盒子的侧面积为S的值能否是60cm2,若能,请求出x的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赣县田村素称“灯彩之乡”,田村花灯源于唐代,盛于宋朝,迄今已有1300多年历史了,某公司生产了一种田村花灯,每件田村花灯制造成本为20元.设销售单价x(元),每日销售量y(件)、每日的利润w(元).在试销过程中,每日销售量y(件)、每日的利润w(元)与销售单价x(元)之间存在一定的关系,其几组对应量如下表所示:
销售单价x(元) | 30 | 31 | 32 | 40 |
销售量y(件) | 40 | 38 | 36 | 20 |
(1)根据表中数据的规律、分別写出每日销售量y(件)、每日利润w(元)关于销售单价x(元)之间的函数表达式(利润=(销售单价﹣成本单价)×销售件数).
(2)当销售单价为多少元时,公司每日能够获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】布袋里有四个小球,球表面分别标有2、3、4、6四个数字,它们的材质、形状、大小完全相同。从中随机摸出一个小球记下数字为x,再从剩下的三个球中随机摸出一个球记下数字为y,点A的坐标为(x,y).运用画树状图或列表的方法,写出A点所有可能的坐标,并求出点A在反比例函数![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
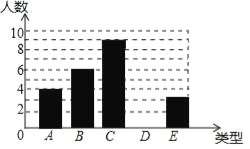
【题目】某校初一年级随机抽取30名学生,对5种活动形式:A、跑步,B、篮球,C、跳绳,D、乒乓球,E、武术,进行了随机抽样调查,每个学生只能选择一种运动行驶,调查统计结果,绘制了不完整的统计图.
(1)将条形图补充完整;
(2)如果初一年级有900名学生,估计喜爱跳绳运动的有多少人?
(3)某次体育课上,老师在5个一样的乒乓球上分别写上A、B、C、D、E,放在不透明的口袋中,每人每次摸出一个球并且只摸一次,然后放回,按照球上的标号参加对应活动,小明和小刚是好朋友,请用树状图或列表法的方法,求他俩恰好是同一种活动形式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与y轴交于点A,点B是抛物线上的一点,过点B作
与y轴交于点A,点B是抛物线上的一点,过点B作![]() 轴于点C,且点C的坐标为
轴于点C,且点C的坐标为![]() .
.
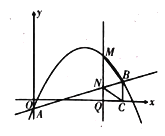
(1)求直线AB的表达式;
(2)若直线![]() 轴,分别与抛物线,直线AB,x轴交于点M、N、Q,且点Q位于线段OC之间,求线段MN长度的最大值;
轴,分别与抛物线,直线AB,x轴交于点M、N、Q,且点Q位于线段OC之间,求线段MN长度的最大值;
(3)当四边形MNCB是平行四边形时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象分别交x轴、y轴于C,D两点,交反比例函数
的图象分别交x轴、y轴于C,D两点,交反比例函数![]() 图象于A(
图象于A(![]() ,4),B(3,m)两点.
,4),B(3,m)两点.
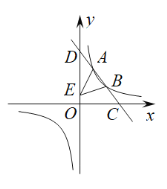
(1)求直线CD的表达式;
(2)点E是线段OD上一点,若![]() ,求E点的坐标;
,求E点的坐标;
(3)请你根据图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
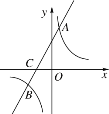
【题目】如图,直线y1=ax+b与反比例函数y2=![]() 交于A,B两点,与x轴交于点C,点A的纵坐标为6,点B的坐标为(-3,-2).
交于A,B两点,与x轴交于点C,点A的纵坐标为6,点B的坐标为(-3,-2).
(1)求直线和反比例函数的解析式;
(2)求点C的坐标,并结合图象直接写出y1<0时x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com