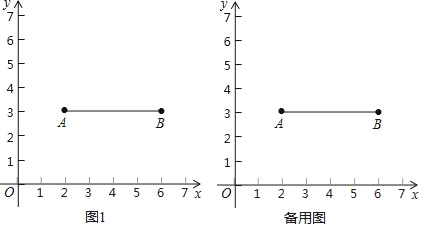
【题目】如图，在平面直角坐标系中，给出如下定义：已知点A（2，3），点B（6，3），连接AB．如果线段AB上有一个点与点P的距离不大于1，那么称点P是线段AB的“环绕点”．

（1）已知点C（3，1.5），D（4，3.5），E（1，3），则是线段AB的“环绕点”的点是　 　；

（2）已知点P（m，n）在反比例函数y=的图象上，且点P是线段AB的“环绕点”，求出点P的横坐标m的取值范围；

（3）已知⊙M上有一点P是线段AB的“环绕点”，且点M（4，1），求⊙M的半径r的取值范围．

参考答案：

【答案】（1）点D和E（2）2≤m≤4；（3）1≤r≤2+1

【解析】分析：（1）根据点A、B的纵坐标相等判断出AB∥x轴，然后求出点C、D、E到AB的距离，再根据“环绕点”的定义判断；
（2）当点P在线段AB的上方，当点P在线段AB的下方，根据点P到线段AB的距离为1时，即可得到结论；
（3）当点P在线段AB的下方时，且到线段AB的最小距离是1时，当点P在线段AB的上方时，且到点A的距离是1时，即可得到结论．

详解：(1)由“环绕点”的定义可知：点P到直线AB的距离d应满足：

∵A、B两点的纵坐标都是3，

∴AB∥x轴，

∴点C到直线AB的距离为|1.53|=1.5>1，

点D到直线AB的距离为|3.53|=0.5<1，

点E到直线AB的距离为|33|=0<1，

∴点D和E是线段AB的环绕点；

故答案为：点D和E；

(2)当点P在线段AB的上方，点P到线段AB的距离为1时，m=2；

当点P在线段AB的下方，点P到线段AB的距离为1时，m=4；

所以点P的横坐标m的取值范围为：

(3)当点P在线段AB的下方时，且到线段AB的最小距离是1时，r=1；

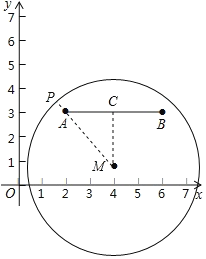
当点P在线段AB的上方时，且到点A的距离是1时，如图，过M作MC⊥AB，

则CM=2，AC=2，

连接MA并延长交⊙M于P，

则PA=1，

∴,即

∴⊙M的半径r的取值范围是

关闭