
【题目】如图,一次函数y=﹣x+4的图象与反比例y=![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求PA+PB的最小值.

【答案】(1)y=![]() ;点B坐标(3,1);(2)2
;点B坐标(3,1);(2)2![]() .
.
【解析】
(1)把点A(1,a)代入一次函数y=-x+4,即可得出a,再把点A坐标代入反比例函数y=![]() ,即可得出k,两个函数解析式联立求得点B坐标;
,即可得出k,两个函数解析式联立求得点B坐标;
(2)作点B作关于x轴的对称点D,连接AD,交x轴于点P,此时PA+PB=PA+PD=AD的值最小,然后根据勾股定理即可求得.
(1)把点A(1,a)代入一次函数y=﹣x+4,
得a=﹣1+4,
解得a=3,
∴A(1,3),
点A(1,3)代入反比例函数y=![]() ,
,
得k=3,
∴反比例函数的表达式y=![]() ,
,
两个函数解析式联立列方程组得
解得x1=1,x2=3,
∴点B坐标(3,1);
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB=PA+PD=AD的值最小,
∴D(3,﹣1),
∵A(1,3),
∴AD=![]() =2
=2![]() ,
,
∴PA+PB的最小值为2![]() .
.


科目:初中数学 来源: 题型:
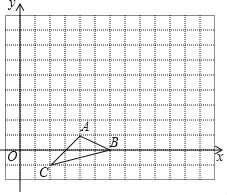
【题目】(1)将△ABC沿x轴负方向平移2个单位,沿y轴正方向平移4个单位,得到△A1B1C1,请画出△A1B1C1.
(2)将△ABC绕点A顺时针旋转90°,得到△AB2C2,请画出△AB2C2.
(3)△A1B1C1绕点P顺时针旋转90°,得到△AB2C2,则点P的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为![]() .
.
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,
求两次摸 出都是红球的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC是⊙O的直径,B为⊙O上一点,D为![]() 的中点,过D作EF∥BC交AB的延长线于点E,交AC的延长线于点F.
的中点,过D作EF∥BC交AB的延长线于点E,交AC的延长线于点F.
(Ⅰ)求证:EF为⊙O的切线;
(Ⅱ)若AB=2,∠BDC=2∠A,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆低端D到大楼前梯砍底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:![]() ,则大楼AB的高度为_________米.
,则大楼AB的高度为_________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.

(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展以素质提升为主题的研学活动,推出了以下四个项目供学生选择:A.模拟驾驶;B.军事竞技;C.家乡导游;D.植物识别.学校规定:每个学生都必须报名且只能选择其中一个项目.八年级(3)班班主任宁老师对全
班学生选择的项目情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
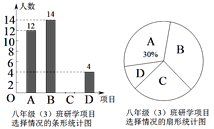
(1)八年级(3)班学生总人数是多少,并将条形统计图补充完整;
(2)宁老师发现报名参加“植物识别”的学生中恰好有两名男生,现准备从这组学生中任意挑选两名担任活动记录员,那么恰好选1名男生和1名女生担任活动记录员的概率;
(3)若学校学生总人数为2000人,根据八年级(3)班的情况,估计全校报名军事竞技的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
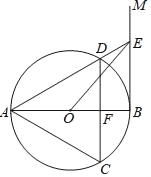
【题目】如图,AB是⊙O的直径,过点B作⊙O的切线BM,点A,C,D分别为⊙O的三等分点,连接AC,AD,DC,延长AD交BM于点E,CD交AB于点F.
(1)求证:CD∥BM;
(2)连接OE,若DE=m,求△OBE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是一张简易活动餐桌,测得OA=OB=30cm,OC=OD=50cm,现要求桌面离地面的高度为40cm,那么两条桌脚的张角∠COD的度数大小应为( )
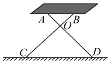
A. 100° B. 120° C. 135° D. 150°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com