
⑴操作:如图23-1,O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心角为直角的扇形纸板的圆心放在O点处,并将纸板绕O点旋转.
求证:正方形ABCD的边被纸板覆盖部分的总长度为定值a.
⑵思考:如图23-2,将一块半径足够长的扇形纸板的圆心放在边长为a的正三角形或边长为a的正五边形的中心O点处,并将纸板绕O点旋转.当扇形纸板的圆心角为__________时,正三角形的边被纸板覆盖部分的总长度为定值a;如图23-3,当扇形纸板的圆心角为_________时,正五边形的边被纸板覆盖部分的总长度为定值a.(直接填空)
⑶探究:一般地,将一块半径足够长的扇形纸板的圆心放在边长为a的正n边形的中心O点处,并将纸板绕O点旋转,当扇形纸板的圆心角为________度时,正n边形的边被纸板覆盖部分的总长度为定值a;
这时正n边形被纸板覆盖部分的面积是否也为定值?若为定值,写出它与正n边形面积S之间的关系(不需证明);若不是定值,请说明理由。

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
| ||
| 3 |
| ||
| 3 |
| 3 |
| 3 |
 n为正整数)次这样的操作菱形中心O所经过的路径总长为
n为正整数)次这样的操作菱形中心O所经过的路径总长为2
| ||
| 3 |
2
| ||
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
已知:矩形纸片ABCD中,AB=26厘米,BC=18.5厘米,点E在AD上,且AE=6厘米,点P是![]() 边上一动点.按如下操作:
边上一动点.按如下操作:
步骤一,折叠纸片,使点P与点![]() 重合,展开纸片得折痕MN(如图23(1)所示);
重合,展开纸片得折痕MN(如图23(1)所示);
步骤二,过点P作![]() ,交MN所在的直线于点Q,连接QE(如图23(2)所示)
,交MN所在的直线于点Q,连接QE(如图23(2)所示)
(1)无论点P在![]() 边上任何位置,都有PQ QE(填“
边上任何位置,都有PQ QE(填“![]() ”、“
”、“![]() ”、“
”、“![]() ”号);
”号);
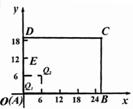
(2)如图23(3)所示,将纸片ABCD放在直角坐标系中,按上述步骤一、二进行操作:
①当点![]() 在
在![]() 点时,PT与MN交于点Q1 ,Q1点的坐标是( , );
点时,PT与MN交于点Q1 ,Q1点的坐标是( , );
②当PA=6厘米时,PT与MN交于点Q2 ,Q2点的坐标是( , );
③当PA=12厘米时,在图22(3)中画出MN,PT(不要求写画法),并求出MN与PT的交点Q3的坐标;
(3)点![]() 在运动过程中,PT与MN形成一系列的交点Q1 ,Q2 ,Q3 ,…观察、猜想:众多的交点形成的图象是什么?并直接写出该图象的函数表达式.
在运动过程中,PT与MN形成一系列的交点Q1 ,Q2 ,Q3 ,…观察、猜想:众多的交点形成的图象是什么?并直接写出该图象的函数表达式.
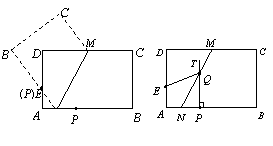 |
23(1) 23(2) 23(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
⑴操作:如图23-1,O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心角为直角的扇形纸板的圆心放在O点处,并将纸板绕O点旋转.
求证:正方形ABCD的边被纸板覆盖部分的总长度为定值a.
⑵思考:如图23-2,将一块半径足够长的扇形纸板的圆心放在边长为a的正三角形或边长为a的正五边形的中心O点处,并将纸板绕O点旋转.当扇形纸板的圆心角为__________时,正三角形的边被纸板覆盖部分的总长度为定值a;如图23-3,当扇形纸板的圆心角为_________时,正五边形的边被纸板覆盖部分的总长度为定值a.(直接填空)
⑶探究:一般地,将一块半径足够长的扇形纸板的圆心放在边长为a的正n边形的中心O点处,并将纸板绕O点旋转,当扇形纸板的圆心角为________度时,正n边形的边被纸板覆盖部分的总长度为定值a;
这时正n边形被纸板覆盖部分的面积是否也为定值?若为定值,写出它与正n边形面积S之间的关系(不需证明);若不是定值,请说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com