
【题目】已知在菱形ABCD中,∠ABC=60°,M、N分别是边BC,CD上的两个动点,∠MAN=60°,AM、AN分别交BD于E、F两点.

(1)如图1,求证:CM+CN=BC;
(2)如图2,过点E作EG∥AN交DC延长线于点G,求证:EG=EA;
(3)如图3,若AB=1,∠AED=45°,直接写出EF的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)如图1中,在AC上截取CG,使得CG=CM.首先证明△BAM≌△CAN,推出AM=AN,△AMN是等边三角形,再证明△AMG≌△NMC即可解决问题;(2)如图2中,想办法证明AE=EC,EC=EG即可解决问题;(3)如图3中,将△ABE绕点A逆时针旋转120°得到△ADQ,首先证明△FQD是特殊直角三角形,设DQ=x,构建方程即可解决问题;
(1)证明:如图1中,在AC上截取CG,使得CG=CM.
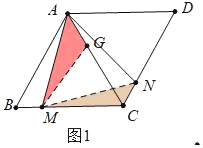
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC,△ACD都是等边三角形,
∴∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
∵AB=AC,∠B=∠ACN=60°,
∴△BAM≌△CAN,
∴AM=AN,
∵∠MAN=60°,
∴△AMN是等边三角形,
∵CM=CG,∠MCG=60°,
∴△CMG是等边三角形,
∴MA=MN,MG=MC,
∵∠AMN=∠GMC=60°,
∴∠AMG=∠NMC,
∴△AMG≌△NMC,
∴AG=CN,
∴BC=AC=CG+AG=CM+CN,
即BC=CM+CN.
(2)证明:如图2中,连接EC.
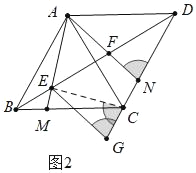
∵BA=BC,∠ABE=∠CBE,BE=BE,
∴△ABE≌△CBE,
∴AE=EC,∠BAE=∠BCE,
∵EG∥AN,
∴∠G=∠AND,
∵∠AND=∠CAN+∠ACN=60°+∠CAN,∠ECG=60°+∠ECB,
∵∠ECB=∠BAE=∠CAN,
∴∠ECG=∠AND=∠G,
∴EC=EG,
∴EA=EG.
(3)解:如图3中,将△ABE绕点A逆时针旋转120°得到△ADQ,
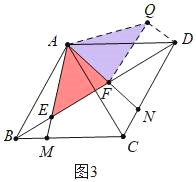
易证△AFE≌△AFQ,
∴∠AEF=∠AQF=45°,
∵∠AEB=∠AQD=135°,
∴∠FQD=90°,
∵∠QDF=∠ADQ+∠ADF=60°,设DQ=BE=x,则DF=2x,EF=FQ=![]() x,
x,
∵AB=AD=1,∠ABD=30°,
∴BD=![]() ,
,
∴x+2x+![]() x=
x=![]() ,
,
∴x=![]() ,
,
∴EF=![]() x=
x=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图所示,△ABC为等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,有下列四个结论:①点P在∠BAC的平分线上;②AS=AR;③QP∥AB;④△BRP≌△CSP.其中,正确的有__________(填序号即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),( ![]() ,y2)是抛物线上两点,则y1<y2 , 其中说法正确的是( )
,y2)是抛物线上两点,则y1<y2 , 其中说法正确的是( ) 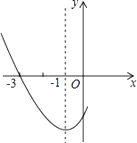
A.①②
B.②③
C.①②④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD,把△BCD沿BD翻折,得△BDG,BG,AD所在的直线交于点E,过点D作DF∥BE交BC所在直线于点F.

(1)如图1,AB<AD,
①求证:四边形BEDF是菱形;
②若AB=4,AD=8,求四边形BEDF的面积;
(2)如图2,若AB=8,AD=4,请按要求画出图形,并直接写出四边形BEDF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列语句,设适当的未知数,列出二元一次方程:
![]() 甲数比乙数的
甲数比乙数的![]() 倍少
倍少![]() ;
;
![]() 甲数的
甲数的![]() 倍与乙数的
倍与乙数的![]() 倍的和是
倍的和是![]() ;
;
![]() 甲数的
甲数的![]() 与乙数的
与乙数的![]() 的差是
的差是![]() ;
;
![]() 甲数与乙数的和的
甲数与乙数的和的![]() 倍比乙数与甲数差的
倍比乙数与甲数差的![]() 多
多![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠B=∠D,BC=DC,要判定△ABC≌△EDC,当添加条件_________时,可根据“ASA”判定;当添加条件_____时,可根据“AAS”判定;当添加条件________时,可根据“SAS”判定.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com