练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

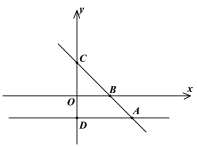
    【题目】如图，在平面直角坐标系中，直线y=﹣x+m过点A（5，—2）且分别与x轴、y轴交于点B、C，过点A画AD//x轴，交y轴于点D．

    （1）求点B、C的坐标；

    （2）在线段AD上存在点P，使BP+ CP最小，求点P的坐标．

    【答案】（1），；（2）．

    【解析】

    （1）代入点A(5,-2)求出m的值，分别代入y=0和x=0，求出点B、C的坐标

    （2）过C作直线AD对称点Q，求出直线BQ的方程式，代入y=-2，即可求出点P的坐标

    （1）∵y=-x+m过点A(5,-2)，

    ∴-2=-5+m，

    ∴m=3

    ∴y=-x+3

    令y=0，∴x=3，∴B(3，0)

    令x=0，∴y=3，∴C(0，3)

    （2）过C作直线AD对称点Q，可得Q(0，-7) ，

    连结BQ，交AD与点P，

    可得直线BQ:

    令y’= -2∴

    ∴

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】直线经过原点和点，点的坐标为.

    (1)求直线所对应的函数解析式;

    （2）当P在线段OA上时，设点横坐标为，三角形的面积为，写出关于的函数解析式，并指出自变量的取值范围；

    （3）当P在射线OA上时，在坐标轴上有一点,使（正整数），请直接写出点的坐标（本小题只要写出结果，不需要写出解题过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数y＝kx＋b的图象与反比例函数y＝ (x＞0)的图象交于点P(n，2)，与x轴交于点A(－4，0)，与y轴交于点C，PB丄x轴于点B，点A与点B关于y轴对称．

    （1）求一次函数、反比例函数的解析式；

    （2）求证：点C为线段AP的中点；

    （3）反比例函数图象上是否存在点D，使四边形BCPD为菱形，如果存在，说明理由并求出点D的坐标；如果不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市推出电脑上网包月制，每月收取费用y（元）与上网时间x（小时）的函数关系如图所示，其中BA是线段，且BA∥x轴，AC是射线．

    （1）当x≥30，求y与x之间的函数关系式；

    （2）若小李4月份上网20小时，他应付多少元的上网费用？

    （3）若小李5月份上网费用为75元，则他在该月份的上网时间是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的方程

    （1）当m___________时，已知方程为一元一次方程；

    （2）当m___________时，已知方程为一元二次方程；

    （3）若已知方程有实数根，求m的取值范围。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

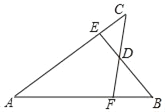
    【题目】如图，已知AB＝AC，AE＝AF，BE与CF交于点D，则对于下列结论：①△ABE≌△ACF；②△BDF≌△CDE；③D在∠BAC的平分线上．其中正确的是（　　）

    A. ① B. ② C. ①和② D. ①②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学课上，李老师出示了如下框中的题目．

    在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED=EC，如图．试确定线段AE与DB的大小关系，并说明理由．

    小敏与同桌小聪讨论后，进行了如下解答：

    （1）特殊情况，探索结论

    当点E为AB的中点时，如图1，确定线段AE与的DB大小关系．请你直接写出结论：

    AE DB(填“＞”，“＜”或“＝”)．

    图1 图2

    （2）特例启发，解答题目

    解：题目中，AE与DB的大小关系是：AE DB(填“＞”，“＜”或“＝”)．

    理由如下：如图2，过点E作EF∥BC，交AC于点F.

    (请你完成以下解答过程)

    （3）拓展结论，设计新题

    在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED=EC．若△ABC的边长为1，AE=2，求CD的长(请你直接写出结果)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学举行“校园好声音”歌手大赛，初、高中部根据初赛成绩，各选出名选手组成初中代表队和高中代表队参加学校决赛．每个队名选手的决赛成绩如图所示：

    填表：

    平均数（分）

    中位数（分）

    众数（分）

    初中代表队

    高中代表队

    结合两队决赛成绩的平均数和中位数，分析哪个代表队的成绩较好；

    计算两队决赛成绩的方差，并判断哪个代表队的成绩较为稳定．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，和是的半径，并且，是上任一点，的延长线交于点，过点的的切线交延长线于点．

    求证：；

    若，试求的长．

    查看答案和解析>>

    同步练习册答案