
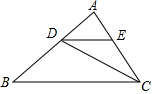
分析 根据角平分线的定义,可得∠ECD=∠BCD,根据等腰三角形的定义,可得∠ECD=∠EDC=∠BCD,再根据平行线的判定,即可得出DE∥BC,然后根据平行线的性质得出∠ABC=∠ADE=40°.
解答 解:解:∵CD是△ABC的角平分线(已知)
∴∠ECD=∠BCD(角平分线的定义)
又∵DE=DC(已知)
∴△CDE是等腰三角形(等腰三角形的定义)
∴∠ECD=∠EDC=∠BCD(等量代换)
∴DE∥BC(内错角相等,两直线平行)
∴∠ABC=∠ADE=40°(两直线平行,同位角相等),
故答案为:已知;角平分线的定义;已知;等腰三角形的定义;等量代换;内错角相等,两直线平行;两直线平行,同位角相等;
点评 本题考查的是平行线的判定与性质的运用,解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系;平行线的性质是由平行关系来寻找角的数量关系.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
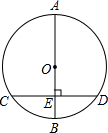 如图,⊙O的直径AB=20cm,CD是⊙O的弦,AB⊥CD,垂足为E,OE:EB=3:2,则CD的长是( )
如图,⊙O的直径AB=20cm,CD是⊙O的弦,AB⊥CD,垂足为E,OE:EB=3:2,则CD的长是( )| A. | 10cm | B. | 14cm | C. | 15cm | D. | 16cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x-y}{x+y}$=-$\frac{y-x}{y+x}$ | B. | $\frac{-a-b}{a+b}$=-1 | C. | $\sqrt{{(1-\sqrt{2})}^{2}}$=$\sqrt{2}$-1 | D. | $\sqrt{{a}^{2}}$=a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2000 | |
| B. | 湖州市2017年中考数学成绩 | |
| C. | 被抽取的2000名考生 | |
| D. | 被抽取的2000名考生的中考数学成绩 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1000 | B. | 1000名 | ||
| C. | 43735名考生的数学成绩 | D. | 1000名考生的数学成绩 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
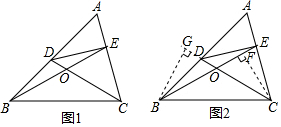 我们知道有两条边相等的三角形叫做等腰三角形.类似的,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
我们知道有两条边相等的三角形叫做等腰三角形.类似的,我们定义:至少有一组对边相等的四边形叫做等对边四边形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com