
【题目】某公司改革实行每月考核再奖励的新制度,大大调动了员工的积极性,![]() 年一名员工每月奖金的变化如下表:(正数表示比前一月多的钱数,负数表示比前一月少的钱数)单位:(元)
年一名员工每月奖金的变化如下表:(正数表示比前一月多的钱数,负数表示比前一月少的钱数)单位:(元)
月份 | 一月 | 二月 | 三月 | 四月 | 五月 | 六月 | 七月 |
钱数变化 |
|
|
|
|
|
|
|
(1)若![]() 年底
年底![]() 月份奖金为
月份奖金为![]() 元,用代数式表示
元,用代数式表示![]() 年二月的奖金;
年二月的奖金;
(2)请判断七个月以来这名员工得到奖金最多是哪个月?最少是哪个月?他们相差多少元?
(3)若![]() 年这七个月中这名员工最多得到的奖金是
年这七个月中这名员工最多得到的奖金是![]() 元,请问
元,请问![]() 年
年![]() 月份他得到多少奖金?
月份他得到多少奖金?
【答案】(1)![]() 元;(2)最多的是七月份,最少的是四月份,810元;(3)1720元
元;(2)最多的是七月份,最少的是四月份,810元;(3)1720元
【解析】
(1)根据题意和表格中的数据可以表示出二月份的奖金;
(2)根据表格中的数据可以表示出2019年前七个月的奖金,从而可以解答本题;
(3)根据(2)中的七月份的奖金可以求得a的值,从而可以解答本题.
(1)由题意可得:
2019年二月的奖金是:a+300+220=(a+520)(元),
即2019年二月的奖金是(a+520)元;
(2)由题意可得:
一月份奖金为:(a+300)元,
二月份奖金为:a+300+220=(a+520)元,
三月份奖金为:a+520﹣150=(a+370)元,
四月份奖金为:a+370﹣100=(a+270)元,
五月份奖金为:a+270+330=(a+600)元,
六月份奖金为:a+600+200=(a+800)元,
七月份奖金为:a+800+280=(a+1080)元,
由上可得:最多的是七月份,最少的是四月份,它们的差是:(a+1080)﹣(a+270)=810(元),
即七个月以来这名员工得到奖金最多七月,最少是四月,它们相差810元;
(3)由题意可得:
a+1080=2800,
解得:a=1720,
即2018年12月份他得到1720元奖金.


科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
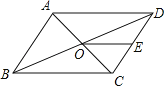
A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果抛物线C: y=ax2+bx+c(a≠0)与直线l:y=kx+d(k≠0)都经过y轴上一点P,且抛物线C的顶点Q在直线l上,那么称此直线l与该抛物线C具有“一带一路”关系.如果直线y=mx+1与抛物线y=x2-2x+n具有“一带一路”关系,那么m+n=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解高中学生每月用掉中性笔笔芯的情况,随机抽查了30名高中学生进行调查,并将调查的数据制成如下的表格:
月平均用中性笔笔芯(根) | 4 | 5 | 6 | 7 | 8 | 9 |
被调查的学生数 | 7 | 4 | 9 | 5 | 2 | 3 |
请根据以上信息,解答下列问题:
(1)被调查的学生月平均用中性笔笔芯数大约________根;
(2)被调查的学生月用中性笔笔芯数的中位数为________根,众数为________根;
(3)根据样本数据,若被调查的高中共有1000名学生,试估计该校月平均用中性笔笔芯数9根的约多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以直线MN上的线段BC为边作正方形ABCD,CH平分∠DCN,点E为射线BN上一点,连接AE,过点E作AE的垂线交射线CH于点F,探索AE与EF的数量关系。
(1)阅读下面的解答过程。并按此思路完成余下的证明过程
当点E在线段BC上,且点E为BC中点时,AB=EF
理由如下:
取AB中点P,達接PE
在正方形ABCD中,∠B=∠BCD=90°,AB=BC
∴△BPE等腰三角形,AP=BC
∴∠BPB=45°
∴∠APBE=135°
又因为CH平分∠DCN
∴∠DCF=45°
∴∠ECF=135°
∴∠APE=∠ECF
余下正明过程是:
(2)当点E为线段AB上任意一点时,如图2,结论“AE=EF”是否成立,如果成立,请给出证明过程;
(3)当点E在BC的延长线时,如图3,结论“AE=EF”是否仍然成立,如果成立,请在图3中画出必要的辅助线(不必说明理由)。
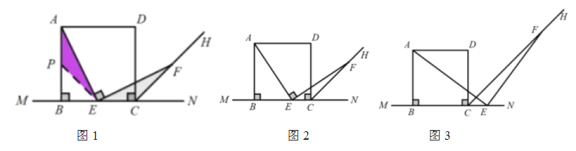
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克,为了促销,该经营户决定降价销售,经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克,另外,每天的房租等固定成本共24元,设每千克降价x元每天销量为y千克.
(1)求y与x的函数关系式;
(2)如何定价,才能使每天获得的利润为200元,且使每天的销量较大?
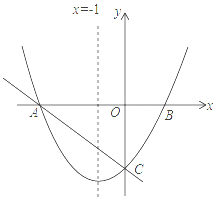
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知
与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知![]() ,
,![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 在抛物线的对称轴上是否存在点P,使
在抛物线的对称轴上是否存在点P,使![]() 是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
![]() 点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,
点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,![]() 的面积最大?求出
的面积最大?求出![]() 的最大面积及此时E点的坐标.
的最大面积及此时E点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
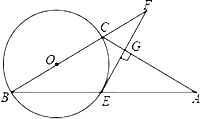
【题目】如图,已知△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.
(1)求证:FE是⊙O的切线;
(2)若FE=4,FC=2,求⊙O的半径及CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com