
分析 把x-y=1化为x=y+1,代入方程①,求出y,再把y值代入x=y+1,求出x即可.
解答 解:由②得:x=y+1 ③,
把③代入①得:(y+1)2-2y2=-2,
即y2-2y-3=0,
解得:y1=-1,y2=3,
把y1=-1,y2=3代入③得x1=0,x2=4.
故方程组的解为$\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{1}=-1}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=4}\\{{y}_{2=3}}\end{array}\right.$.
点评 本题考查的是二元二次方程组的解法,把其中的二元一次方程变形,用一个未知数表示另一个未知数,代入二元二次方程,得到一个一元二次方程,解出未知数,代入求解,得到原方程组的解.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:初中数学 来源: 题型:解答题
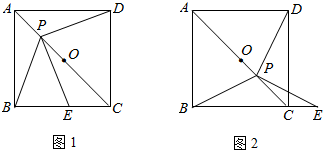
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
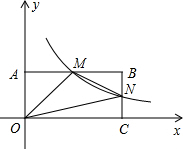 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(6,3),直线y=-$\frac{1}{2}$x+4交AB,BC分别于点M,N,反比例函数y=$\frac{k}{x}$的图象经过点M,N.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(6,3),直线y=-$\frac{1}{2}$x+4交AB,BC分别于点M,N,反比例函数y=$\frac{k}{x}$的图象经过点M,N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
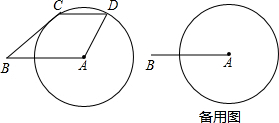
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
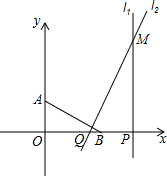 如图,点A(0,2)、B(4,0),点P从(8,0)出发,以每秒2个单位长度沿x轴向坐标原点O匀速运动,同时,点Q从B点出发,以每秒1个单位长度沿x轴向坐标原点O匀速运动,过点P作x轴的垂线l,过点Q作AB的垂线l2,它们的交点为M.设运动的时间为t(0<t<4)秒
如图,点A(0,2)、B(4,0),点P从(8,0)出发,以每秒2个单位长度沿x轴向坐标原点O匀速运动,同时,点Q从B点出发,以每秒1个单位长度沿x轴向坐标原点O匀速运动,过点P作x轴的垂线l,过点Q作AB的垂线l2,它们的交点为M.设运动的时间为t(0<t<4)秒查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com