
【题目】已知![]() ,
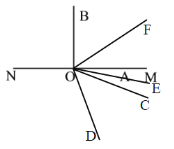
,![]() ,按如图1所示摆放,将OA、OC边重合在直线MN上,OB、OD边在直线MN的两侧;
,按如图1所示摆放,将OA、OC边重合在直线MN上,OB、OD边在直线MN的两侧;



(1)保持![]() 不动,将
不动,将![]() 绕点O旋转至如图2所示的位置,则①
绕点O旋转至如图2所示的位置,则①![]() = ;②
= ;②![]() = ;
= ;
(2)若![]() 按每分钟
按每分钟![]() 的速度绕点O逆时针方向旋转,
的速度绕点O逆时针方向旋转,![]() 按每分钟
按每分钟![]() 的速度也绕点O逆时针方向旋转,OC旋转到射线ON上时都停止运动,设旋转t分钟,计算
的速度也绕点O逆时针方向旋转,OC旋转到射线ON上时都停止运动,设旋转t分钟,计算![]() (用t的代数式表示)。
(用t的代数式表示)。
(3)保持![]() 不动,将
不动,将![]() 绕点O逆时针方向旋转
绕点O逆时针方向旋转![]() ,若射线OE平分
,若射线OE平分![]() ,射线OF平分
,射线OF平分![]() ,求
,求![]() 的大小;
的大小;
【答案】(1)①150°;②30°;(2) 8t-60或2t+60;(3) ∠EOF的大小为15°或165°.
【解析】
(1)①根据∠AOB及∠COD的度数求出∠AOB+∠COD的度数,然后利用角与角之间的关系进行代换化简即可;
②根据∠AOB及∠COD的度数求出∠AOB-∠COD的度数,然后利用角与角之间的关系进行代换化简即可;
(2)分情况讨论:OD与OA相遇前及OD与OA相遇后,画出图形,再根据角与角之间的关系进行计算即可;
(3)分情况讨论,根据角与角之间的关系进行计算即可.
解:(1)①∵∠AOB=90°,∠COD=60°,
∴∠AOB+∠COD=90°+60°=150°,
∵∠AOB=∠AOC+∠BOC,∠COD=∠AOC+∠AOD,
∴∠AOC+∠BOC+∠AOC+∠AOD=150°,
∴∠AOC+∠BOD=150°;
②∵∠AOB=90°,∠COD=60°,
∴∠AOB-∠COD=90°-60°=30°,
∵∠AOB=∠AOC+∠BOC,∠COD=∠AOC+∠AOD,
∴∠AOC+∠BOC-(∠AOC+∠AOD)=30°,
∴∠BOC-∠AOD=30°;
(2)设运动时间为t秒,由题意可知:0<t≤36,∠MOC=5t,∠MOA=2t,
当OD与OA相遇时,5t-2t=60,解得:t=20,
∴经过20秒,OD与OA相遇,
①0<t≤20时,OD与OA相遇前,如图所示,
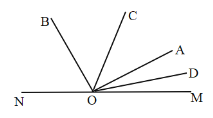
∠AOD=∠COD+∠AOM-∠MOC=60+2t-5t=60-3t,
∴∠MOC-∠AOD=5t-(60-3t)=8t-60;
②20<t≤36时,OD与OA相遇后,如图所示,
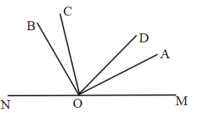
∠AOD=∠MOC-∠COD-∠AOM=5t-60-2t=3t-60,
∴∠MOC-∠AOD=5t-(3t-60)=2t+60;
(3)设OC绕点O逆时针旋转n°,则OD也绕点O逆时针旋转n°,
①0<n°≤150°时,射线OE、OF在射线OB同侧,在直线MN同侧,

∵∠BOD=150°-n°,∠AOC=n°,OE平分∠AOC,OF平分∠BOD,
∴∠BOF=![]() (150°-n°),∠BOE=90°-
(150°-n°),∠BOE=90°-![]() n°,
n°,
∴∠EOF=∠BOE-∠BOF=15°;
②150°<n°≤180°时,射线OE、OF在射线OB异侧,在直线MN同侧,
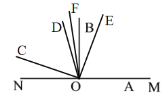
∵∠BOD= n°-150°,∠AOC=n°,OE平分∠AOC,OF平分∠BOD,
∴∠BOF=![]() (n°-150°),∠BOE=90°-
(n°-150°),∠BOE=90°-![]() n°,
n°,
∴∠EOF=∠BOE+∠BOF=15°;
③180°<n°≤330°时,射线OE、OF在射线OB异侧,在直线MN异侧,
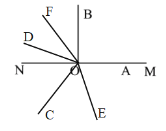
∵∠BOD= n°-150°,∠AOC=360°-n°,OE平分∠AOC,OF平分∠BOD,
∴∠DOF=![]() (n°-150°),∠COE=
(n°-150°),∠COE=![]() (360°-n°),
(360°-n°),
∴∠EOF=∠DOF+∠COD+∠COE=165°;
④330°<n°≤360°时,射线OE、OF在射线OB同侧,在直线MN异侧,
∵∠BOD=360°-(n°-150°),∠AOC=360°-n°,OE平分∠AOC,OF平分∠BOD,
∴∠DOF=![]() [360°-(n°-150°)],∠COE=
[360°-(n°-150°)],∠COE=![]() (360°-n°),
(360°-n°),
∴∠EOF=∠DOF-∠COD-∠COE=15°;
综上,∠EOF的大小为15°或165°.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,点A(m,6),B(n,1)在反比例函数![]() 的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是_____________.
的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
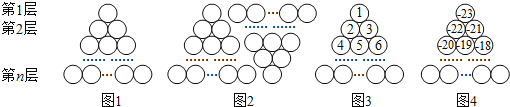
【题目】图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为![]() ,图3图4的中的圆圈共有14层.我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层最左边这个圆圈中的数是__________;我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数﹣23,﹣22,﹣21,…,则图4中所有圆圈中各数的绝对值之和为__________.
,图3图4的中的圆圈共有14层.我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层最左边这个圆圈中的数是__________;我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数﹣23,﹣22,﹣21,…,则图4中所有圆圈中各数的绝对值之和为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠ACB=90°,D是AB的中点,∠EDF=90°
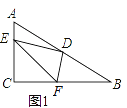
(1)如图1,若E、F分别在AC、BC边上,猜想AE2、BF2和EF2之间有何等量关系,并证明你的猜想;
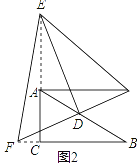
(2)若E、F分别在CA、BC的延长线上,请在图2中画出相应的图形,并判断(1)中的结论是否仍然成立(不作证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,已知直线![]() 与x轴、y轴分别交于A、B两点
与x轴、y轴分别交于A、B两点![]() 直线
直线![]() 直线AB于点
直线AB于点![]() 现有一点P从点D出发,沿线段DO向点O运动,另一点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到O时,两点都停止
现有一点P从点D出发,沿线段DO向点O运动,另一点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到O时,两点都停止![]() 设运动时间为t秒.
设运动时间为t秒.![]() 点A的坐标为______;线段OD的长为______.
点A的坐标为______;线段OD的长为______.![]() 设
设![]() 的面积为S,求S与t之间的函数关系
的面积为S,求S与t之间的函数关系![]() 不要求写出取值范围
不要求写出取值范围![]() ,并确定t为何值时S的值最大?
,并确定t为何值时S的值最大?![]() 是否存在某一时刻t,使得
是否存在某一时刻t,使得![]() 为等腰三角形?若存在,写出所有满足条件的t的值;若不存在,则说明理由.
为等腰三角形?若存在,写出所有满足条件的t的值;若不存在,则说明理由.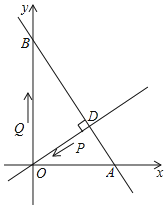
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分别观察下面的左、右两组等式:


根据你发现的规律解决下列问题:
(1)填空:________![]() ;
;
(2)已知![]() ,则x的值是________;
,则x的值是________;
(3)设满足上面特征的等式最左边的数为y,求y的最大值,并写出此时的等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O为△ABC的外接圆,AB=AC,直线MN与⊙O相切于点C,弦BD∥MN,AC与BD相交于点E.

(1)求证:△ABE ≌ △ACD;
(2)若AB = 5,BC = 3,求AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
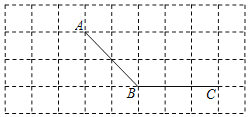
【题目】如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.
![]() 过点C画线段AB的平行线CD;
过点C画线段AB的平行线CD;
![]() 过点A画线段BC的垂线,垂足为E;
过点A画线段BC的垂线,垂足为E;
![]() 过点A画线段AB的垂线,交线段CB的延长线于点F;
过点A画线段AB的垂线,交线段CB的延长线于点F;
![]() 线段AE的长度是点______到直线______的距离;
线段AE的长度是点______到直线______的距离;
![]() 线段AE、BF、AF的大小关系是______
线段AE、BF、AF的大小关系是______![]() 用“
用“![]() ”连接
”连接![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com