
【题目】已知△ABC中,∠ACB=90°,D是AB的中点,∠EDF=90°
(1)如图1,若E、F分别在AC、BC边上,猜想AE2、BF2和EF2之间有何等量关系,并证明你的猜想;
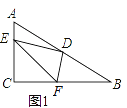
(2)若E、F分别在CA、BC的延长线上,请在图2中画出相应的图形,并判断(1)中的结论是否仍然成立(不作证明)
【答案】(1)结论:AE2+BF2=EF2 ,理由详见解析;(2) 结论不变, AE2+BF2=EF2,证明详见解析.
【解析】
(1)结论:AE2+BF2=EF2.如图1中,延长FD到M,使得DM=DF,连接AM,EM.首先证明△ADM≌△BDF,得到AM=FB,再证明△AEM是直角三角形,理由勾股定理即可解决问题.
(2)结论不变,证明方法类似(1).
(1)结论:AE2+BF2=EF2 .
理由:如图1中,延长FD到M,使得DM=DF,连接AM,EM.

在△ADM和△BDF中,
 ,
,
∴△ADM≌△BDF,
∴AM=BF,∠B=∠MAD,
∵∠C=90°,
∴∠B+∠CAB=90°,
∴∠CAB+∠MAD=90°,即∠EAM=90°,
∵∠EDF=90°,
∴ED⊥FM,∵DM=DF,
∴EM=EF,
在Rt△AEM中,∵AE2+AM2=EM2 ,
∴AE2+BF2=EF2 .
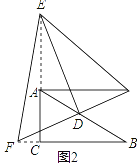
(2)如图2中,结论不变.AE2+BF2=EF2

理由:延长FD到M,使得DM=DF,连接AM,EM.
在△ADM和△BDF中,
 ,
,
∴△ADM≌△BDF,
∴AM=BF,∠B=∠MAD,
∵∠C=90°,
∴∠B+∠CAB=90°,
∴∠CAB+∠MAD=90°,即∠EAM=∠CAM=90°,
∵∠EDF=90°,
∴ED⊥FM,∵DM=DF,
∴EM=EF,
在Rt△AEM中,∵AE2+AM2=EM2 ,
∴AE2+BF2=EF2 .


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
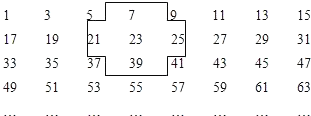
【题目】将连续的奇数1、3、5、7、9、…排成如图的数表,根据题意解答下列问题:
(1)通过观察十字框中5个数的和与中间23满足的关系,发现:若将十字框上下左右平移,可框住另外的5个数也有同样的规律请说出这个规律.
(2)十字框中5个数的和能等于425吗?若能,请写出这5个数,若不能,说明理由.
(3)十字框中5个数的和能等于2020吗?请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解决问题.
(1)在一卷公元前1600年左右遗留下来的古埃及纸草书中,记载着一些数学问题,其中一个问题翻译过来是:“啊哈,它的全部,它的七分之一,其和等于19”.你能求出问题中的“它”吗?
(2)蜘蛛有8条腿,蜻蜓有6条腿.现有蜘蛛、蜻蜓若干只,它们共有120条腿,且蜻蜓的只数是蜘蛛的2倍.你能求出蜘蛛、蜻蜓各多少只吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
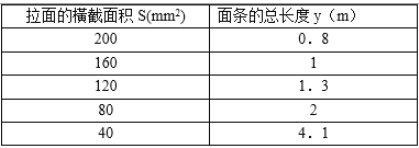
【题目】你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:拉面师傅在一定体积的面团的条件下制做拉面,通过一次又一次地拉长面条,测出每一次拉长面条后面条的总长度与面条的粗细(橫截面积)
(1)请根据表中的数据求出面条的总长度y(m)与面条的粗细(橫截面积) s(mm2)函数关系式;
(2)求当面条粗1.6mm2时,面条的总长度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在长方形纸片ABCD中,E点在边AD上,F、G分别在边AB、CD上,分别以EF、EG为折痕进行折叠并压平,点A、D的对应点分别是点A′和点D′,若ED′平分∠FEG,且![]() 在
在![]() 内部,如图2,设∠A′ED'=n°,则∠FE D′的度数为___________(用含n的代数式表示).
内部,如图2,设∠A′ED'=n°,则∠FE D′的度数为___________(用含n的代数式表示).
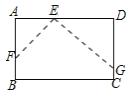
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,按如图1所示摆放,将OA、OC边重合在直线MN上,OB、OD边在直线MN的两侧;
,按如图1所示摆放,将OA、OC边重合在直线MN上,OB、OD边在直线MN的两侧;



(1)保持![]() 不动,将
不动,将![]() 绕点O旋转至如图2所示的位置,则①
绕点O旋转至如图2所示的位置,则①![]() = ;②
= ;②![]() = ;
= ;
(2)若![]() 按每分钟
按每分钟![]() 的速度绕点O逆时针方向旋转,
的速度绕点O逆时针方向旋转,![]() 按每分钟
按每分钟![]() 的速度也绕点O逆时针方向旋转,OC旋转到射线ON上时都停止运动,设旋转t分钟,计算
的速度也绕点O逆时针方向旋转,OC旋转到射线ON上时都停止运动,设旋转t分钟,计算![]() (用t的代数式表示)。
(用t的代数式表示)。
(3)保持![]() 不动,将
不动,将![]() 绕点O逆时针方向旋转
绕点O逆时针方向旋转![]() ,若射线OE平分
,若射线OE平分![]() ,射线OF平分
,射线OF平分![]() ,求
,求![]() 的大小;
的大小;
查看答案和解析>>
科目:初中数学 来源: 题型:
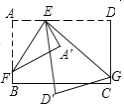
【题目】在求两位数乘两位数时,可以用“列竖式”的方法进行速算,如图给出了部分速算过程.
(1)根据前3个“列竖式”的速算方法,可得a=_____,b=_____,c=_____,d=_____,e=_____,f=_____;
(2)根据前3个“列竖式”的速算方法,在速算“31×![]() ”时,给出了部分过程如图所示.则这个两位数
”时,给出了部分过程如图所示.则这个两位数![]() 可能为_____.
可能为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
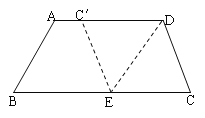
【题目】如图,在梯形纸片ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC于点E,连结C′E.
(1)求证:四边形ECDC′是菱形;
(2)若BC=CD+AD,试判断四边形ABED的形状,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com