
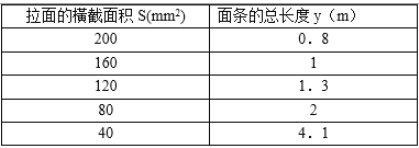
【题目】你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:拉面师傅在一定体积的面团的条件下制做拉面,通过一次又一次地拉长面条,测出每一次拉长面条后面条的总长度与面条的粗细(橫截面积)
(1)请根据表中的数据求出面条的总长度y(m)与面条的粗细(橫截面积) s(mm2)函数关系式;
(2)求当面条粗1.6mm2时,面条的总长度是多少?
【答案】(1)![]() (s>0);(2)当面条粗1.6mm2时,面条的总长度是100m.
(s>0);(2)当面条粗1.6mm2时,面条的总长度是100m.
【解析】
(1)观察表格中的数据可得sy≈160,可把总长度y(m)与面条的粗细(橫截面积) s(mm2)近似的看作反比例函数关系,设面条的总长度y(m)与面条的粗细(橫截面积) s(mm2)函数关系式![]() ,利用待定系数法求得k值,即可求得面条的总长度y(m)与面条的粗细(橫截面积) s(mm2)函数关系式;(2)把s=1.6mm2代入(1)中的解析式即可求解.
,利用待定系数法求得k值,即可求得面条的总长度y(m)与面条的粗细(橫截面积) s(mm2)函数关系式;(2)把s=1.6mm2代入(1)中的解析式即可求解.
(1)观察表格中的数据可得sy≈160,可把总长度y(m)与面条的粗细(橫截面积) s(mm2)近似的看作反比例函数关系,
设面条的总长度y(m)与面条的粗细(橫截面积) s(mm2)函数关系式![]() ,
,
把y=0.8,s=200代入得,![]() ,
,
解得k=160,
∴面条的总长度y(m)与面条的粗细(橫截面积) s(mm2)函数关系式![]() (s>0).
(s>0).
(2)把s=1.6mm2代入![]() 可得,
可得,![]() m.
m.
∴当面条粗1.6mm2时,面条的总长度是100m.


科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与射线
与射线![]() 平行,
平行,![]() .点
.点![]() 是直线
是直线![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() .作
.作![]() 交直线
交直线![]() 于点
于点![]() 平分
平分![]() ,点
,点![]() 都在点
都在点![]() 的右侧.
的右侧.

![]() 求
求![]() 的度数;
的度数;
![]() 若
若![]() ,求
,求![]() 的度数;
的度数;
![]() 把题中条件“射线
把题中条件“射线![]() ”改为“直线
”改为“直线![]() ” ,条件点
” ,条件点![]() 都在点
都在点![]() 的右侧”改为“点
的右侧”改为“点![]() ,
,![]() ,都在点
,都在点![]() 的左侧”,请你在图2中画出
的左侧”,请你在图2中画出![]() ,并直接写出
,并直接写出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐场每天的赢利额y(元)与售出的门票x(张)之间的函数关系如图所示.
(1)当0≤x≤200,且x为整数时,y关于x的函数解析式为【1】;当200≤x≤300,且x为整数时,y关于x的函数解析式为【2】;
(2)要使游乐场一天的赢利超过1000元,试问该天至少应售出多少张门票;
(3)请思考并解释图象与y轴交点(0,﹣1000)的实际意义;
(4)根据图象,请你再提供2条信息.

查看答案和解析>>
科目:初中数学 来源: 题型:
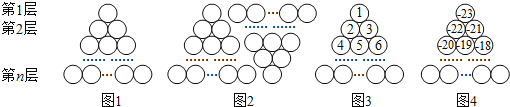
【题目】图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为![]() ,图3图4的中的圆圈共有14层.我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层最左边这个圆圈中的数是__________;我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数﹣23,﹣22,﹣21,…,则图4中所有圆圈中各数的绝对值之和为__________.
,图3图4的中的圆圈共有14层.我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层最左边这个圆圈中的数是__________;我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数﹣23,﹣22,﹣21,…,则图4中所有圆圈中各数的绝对值之和为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你会玩“24点”游戏吗?从一副扑克牌(去掉大、小王)中任意抽取四张,根据牌面上的数字进行混合运算(每一张牌必须用一次且只能用一次,可以加括号),使得运算结果为24或﹣24,其中红色扑克牌代表负数,黑色扑克牌代表正数.J.Q.K.A分别代表11.12.13.1,小明抽到了黑桃7,黑桃3,梅花3,梅花7,他运用下面的方法凑成了:![]() .
.
(1)如果抽到的是黑桃7,黑桃5,红桃5,梅花7,你能凑成24吗?
(2)如果抽到的是黑桃A,方块2,黑桃2,黑桃3,你能凑成24吗?(请用两种方法)
(3)如果抽到的是黑桃Q,红桃Q,梅花3,方块A,你能凑成24吗?(请用多种方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
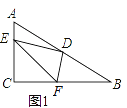
【题目】已知△ABC中,∠ACB=90°,D是AB的中点,∠EDF=90°
(1)如图1,若E、F分别在AC、BC边上,猜想AE2、BF2和EF2之间有何等量关系,并证明你的猜想;
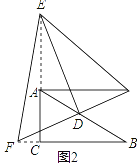
(2)若E、F分别在CA、BC的延长线上,请在图2中画出相应的图形,并判断(1)中的结论是否仍然成立(不作证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分别观察下面的左、右两组等式:


根据你发现的规律解决下列问题:
(1)填空:________![]() ;
;
(2)已知![]() ,则x的值是________;
,则x的值是________;
(3)设满足上面特征的等式最左边的数为y,求y的最大值,并写出此时的等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P是数轴上表示-2与-1两数的点为端点的线段的中点.
![]()
(1)数轴上点P表示的数为 ;
(2)在数轴上距离点P为2.5个单位长度的点表示的数为 ;
(3)如图,若点P是线段AB(点A在点B的左侧)的中点,且点A表示的数为m,那么点B表示的数是 .(用含m的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com