
【题目】在求两位数乘两位数时,可以用“列竖式”的方法进行速算,如图给出了部分速算过程.
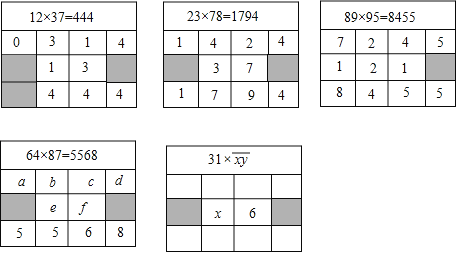
(1)根据前3个“列竖式”的速算方法,可得a=_____,b=_____,c=_____,d=_____,e=_____,f=_____;
(2)根据前3个“列竖式”的速算方法,在速算“31×![]() ”时,给出了部分过程如图所示.则这个两位数
”时,给出了部分过程如图所示.则这个两位数![]() 可能为_____.
可能为_____.
【答案】4 8 2 8 7 4 15或28
【解析】
(1)先找出第二行、第三行、第四行的规律,即可得出结论;
(2)根据规律,建立方程y=3x+2,再利用1≤x≤9,0≤y≤9的整数,确定出x,y的值,即可得出结论.
解:(1)由题意得,第二行的前两格是,两个十位数字相乘,积如果是一位数前面补0,后两格是,两个个位数字相乘,积如果是一位数前面补0,如:2×7=14,3×8=24,
第三行的前三格是,第一个两位数字的个位数字乘以第二个两位数的十位数字再加上第一个两位数的十位数字乘以第二个两位数的个位数字,如图:2×8+3×7=16+21=37,
第四行,同列的两个数相加,如果大于9,进一位;
64×87=5568,6×8=48,4×7=28,6×7+4×8=42+32=74,
如图,
所以,a=4,b=8,c=2,d=8,e=7,f=4,
故答案为:4,8,2,8,7,4;
(2)由(1)的规律得,3×y+1×x=10x+6,
∴y=3x+2,
∵x,y是两位数的十位数字和个位数字,
∴1≤x≤9,0≤y≤9的整数,
∴0≤3x+2≤9,
∴﹣![]() ≤x≤
≤x≤![]() ,
,
∴0<x≤![]() ,
,
∴x=1或x=2,
当x=1时,y=5,即:两位数为15,
当x=2时,y=8,即:两位数为28,
即:满足条件的两位数为15或28,
故答案为15或28.


科目:初中数学 来源: 题型:
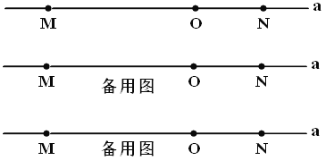
【题目】如图,直线![]() 上有
上有![]() 、
、![]() 两点,
两点,![]() ,点
,点![]() 是线段
是线段![]() 上的一点,
上的一点,![]() .
.
(1)填空:![]() ______
______![]() ,
,![]() ______
______![]() ;
;
(2)若点![]() 是线段
是线段![]() 上一点,且满足
上一点,且满足![]() ,求
,求![]() 的长;
的长;
(3)若动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 两点同时出发,向右运动,点
两点同时出发,向右运动,点![]() 的速度为
的速度为![]() ,点
,点![]() 的速度为
的速度为![]() .设运动时间为
.设运动时间为![]() ,当点
,当点![]() 与点
与点![]() 重合时,
重合时,![]() 、
、![]() 两点停止运动.
两点停止运动.
①当![]() 为何值时,
为何值时,![]() ?
?
②当点![]() 经过点
经过点![]() 时,动点
时,动点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度也向右运动,当点
的速度也向右运动,当点![]() 追上点
追上点![]() 后立即返回,以
后立即返回,以![]() 的速度向点
的速度向点![]() 运动,遇到点
运动,遇到点![]() 后再立即返回,以
后再立即返回,以![]() 的速度向点
的速度向点![]() 运动,如此往返,直到点
运动,如此往返,直到点![]() 、
、![]() 停止运动时,点
停止运动时,点![]() 也停止运动.求出在此过程中点
也停止运动.求出在此过程中点![]() 运动的总路程是多少?
运动的总路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
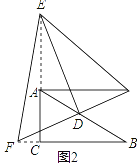
【题目】已知△ABC中,∠ACB=90°,D是AB的中点,∠EDF=90°
(1)如图1,若E、F分别在AC、BC边上,猜想AE2、BF2和EF2之间有何等量关系,并证明你的猜想;
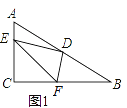
(2)若E、F分别在CA、BC的延长线上,请在图2中画出相应的图形,并判断(1)中的结论是否仍然成立(不作证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,已知直线![]() 与x轴、y轴分别交于A、B两点
与x轴、y轴分别交于A、B两点![]() 直线
直线![]() 直线AB于点
直线AB于点![]() 现有一点P从点D出发,沿线段DO向点O运动,另一点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到O时,两点都停止
现有一点P从点D出发,沿线段DO向点O运动,另一点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到O时,两点都停止![]() 设运动时间为t秒.
设运动时间为t秒.![]() 点A的坐标为______;线段OD的长为______.
点A的坐标为______;线段OD的长为______.![]() 设
设![]() 的面积为S,求S与t之间的函数关系
的面积为S,求S与t之间的函数关系![]() 不要求写出取值范围
不要求写出取值范围![]() ,并确定t为何值时S的值最大?
,并确定t为何值时S的值最大?![]() 是否存在某一时刻t,使得
是否存在某一时刻t,使得![]() 为等腰三角形?若存在,写出所有满足条件的t的值;若不存在,则说明理由.
为等腰三角形?若存在,写出所有满足条件的t的值;若不存在,则说明理由.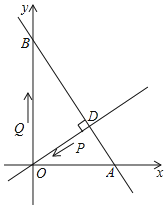
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分别观察下面的左、右两组等式:


根据你发现的规律解决下列问题:
(1)填空:________![]() ;
;
(2)已知![]() ,则x的值是________;
,则x的值是________;
(3)设满足上面特征的等式最左边的数为y,求y的最大值,并写出此时的等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年春节是市民购买葡萄酒的高峰期,某商场分两批购进同一种葡萄酒,第一批所用资金是8000元,第二批所用资金是10000元.第二批葡萄酒每瓶比第一批葡萄酒每瓶贵90元,结果购买数量比第一批少20%.
(1)求该商场两次共购进多少瓶葡萄酒.
(2)第一批葡萄酒的售价是每瓶200元,很快售完,但因为进价的提高第二批葡萄酒的售价在第一批基础上提高了2a%,实际售卖对比第一批少卖a%,结果两次销售共赚得利润3200元,求a(其中a>25).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O为△ABC的外接圆,AB=AC,直线MN与⊙O相切于点C,弦BD∥MN,AC与BD相交于点E.

(1)求证:△ABE ≌ △ACD;
(2)若AB = 5,BC = 3,求AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E在边BC上,且CE=2BE.连接BD、DE、AE,且AE交BD于F,OG为△BDE的中位线.下列结论:①OG⊥CD;②AB=5OG;③![]() ;④BF=OF;⑤
;④BF=OF;⑤![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
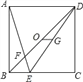
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字﹣3,1,3的不透明卡片,它们除数字外都相同,现将它们背面朝上,洗匀后从三张卡片中随机地抽取一张,放回卡片洗匀后,再从三张卡片中随机地抽取一张.
(1)试用列表或画树状图的方法,求两次抽取的卡片上的数字之积为负数的概率;
(2)求两次抽取的卡片上的数字之和为非负数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com