
【题目】列方程解决问题.
(1)在一卷公元前1600年左右遗留下来的古埃及纸草书中,记载着一些数学问题,其中一个问题翻译过来是:“啊哈,它的全部,它的七分之一,其和等于19”.你能求出问题中的“它”吗?
(2)蜘蛛有8条腿,蜻蜓有6条腿.现有蜘蛛、蜻蜓若干只,它们共有120条腿,且蜻蜓的只数是蜘蛛的2倍.你能求出蜘蛛、蜻蜓各多少只吗?
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购,经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
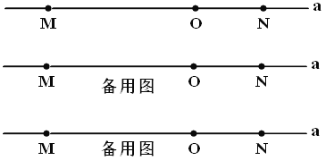
【题目】如图,直线![]() 上有
上有![]() 、
、![]() 两点,
两点,![]() ,点
,点![]() 是线段
是线段![]() 上的一点,
上的一点,![]() .
.
(1)填空:![]() ______
______![]() ,
,![]() ______
______![]() ;
;
(2)若点![]() 是线段
是线段![]() 上一点,且满足
上一点,且满足![]() ,求
,求![]() 的长;
的长;
(3)若动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 两点同时出发,向右运动,点
两点同时出发,向右运动,点![]() 的速度为
的速度为![]() ,点
,点![]() 的速度为
的速度为![]() .设运动时间为
.设运动时间为![]() ,当点
,当点![]() 与点
与点![]() 重合时,
重合时,![]() 、
、![]() 两点停止运动.
两点停止运动.
①当![]() 为何值时,
为何值时,![]() ?
?
②当点![]() 经过点
经过点![]() 时,动点
时,动点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度也向右运动,当点
的速度也向右运动,当点![]() 追上点
追上点![]() 后立即返回,以
后立即返回,以![]() 的速度向点
的速度向点![]() 运动,遇到点
运动,遇到点![]() 后再立即返回,以
后再立即返回,以![]() 的速度向点
的速度向点![]() 运动,如此往返,直到点
运动,如此往返,直到点![]() 、
、![]() 停止运动时,点
停止运动时,点![]() 也停止运动.求出在此过程中点
也停止运动.求出在此过程中点![]() 运动的总路程是多少?
运动的总路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,每个自然数都有因数,对于一个自然数![]() ,我们把小于
,我们把小于![]() 的正的因数叫做
的正的因数叫做![]() 的真因数.如10的正因数有1、2、5、10,其中1、2、5是10的真因数.把一个自然数
的真因数.如10的正因数有1、2、5、10,其中1、2、5是10的真因数.把一个自然数![]() 的所有真因数的和除以
的所有真因数的和除以![]() ,所得的商叫做
,所得的商叫做![]() 的“完美指标”.如10的“完美指标”是
的“完美指标”.如10的“完美指标”是![]() .一个自然数的“完美指标”越接近1,我们就说这个数越“完美”.如8的“完美指标”是
.一个自然数的“完美指标”越接近1,我们就说这个数越“完美”.如8的“完美指标”是![]() ,10的“完美指标”是
,10的“完美指标”是![]() ,因为
,因为![]() 比5更接近1,所以我们说8比10更完美.
比5更接近1,所以我们说8比10更完美.
(1)试计算5的“完美指标”.
(2)试计算6和9的“完美指标”.
(3)试找出15到20的自然数中,最“完美”的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
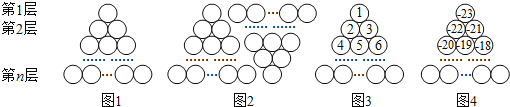
【题目】图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为![]() ,图3图4的中的圆圈共有14层.我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层最左边这个圆圈中的数是__________;我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数﹣23,﹣22,﹣21,…,则图4中所有圆圈中各数的绝对值之和为__________.
,图3图4的中的圆圈共有14层.我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层最左边这个圆圈中的数是__________;我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数﹣23,﹣22,﹣21,…,则图4中所有圆圈中各数的绝对值之和为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象经过点A,且点A到x轴的距离是4.
的图象经过点A,且点A到x轴的距离是4.
(1) 求点A的坐标;
(2) 点![]() 为坐标原点,点
为坐标原点,点![]() 是x轴正半轴上一点,当
是x轴正半轴上一点,当![]() 时,求直线AB的解析式.
时,求直线AB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
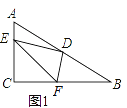
【题目】已知△ABC中,∠ACB=90°,D是AB的中点,∠EDF=90°
(1)如图1,若E、F分别在AC、BC边上,猜想AE2、BF2和EF2之间有何等量关系,并证明你的猜想;
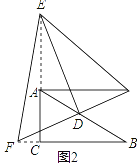
(2)若E、F分别在CA、BC的延长线上,请在图2中画出相应的图形,并判断(1)中的结论是否仍然成立(不作证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,已知直线![]() 与x轴、y轴分别交于A、B两点
与x轴、y轴分别交于A、B两点![]() 直线
直线![]() 直线AB于点
直线AB于点![]() 现有一点P从点D出发,沿线段DO向点O运动,另一点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到O时,两点都停止
现有一点P从点D出发,沿线段DO向点O运动,另一点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到O时,两点都停止![]() 设运动时间为t秒.
设运动时间为t秒.![]() 点A的坐标为______;线段OD的长为______.
点A的坐标为______;线段OD的长为______.![]() 设
设![]() 的面积为S,求S与t之间的函数关系
的面积为S,求S与t之间的函数关系![]() 不要求写出取值范围
不要求写出取值范围![]() ,并确定t为何值时S的值最大?
,并确定t为何值时S的值最大?![]() 是否存在某一时刻t,使得
是否存在某一时刻t,使得![]() 为等腰三角形?若存在,写出所有满足条件的t的值;若不存在,则说明理由.
为等腰三角形?若存在,写出所有满足条件的t的值;若不存在,则说明理由.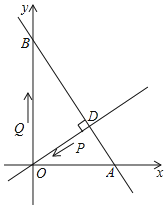
查看答案和解析>>
科目:初中数学 来源: 题型:
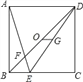
【题目】如图,正方形ABCD中,点E在边BC上,且CE=2BE.连接BD、DE、AE,且AE交BD于F,OG为△BDE的中位线.下列结论:①OG⊥CD;②AB=5OG;③![]() ;④BF=OF;⑤
;④BF=OF;⑤![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com