
【题目】如图,在梯形纸片ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC于点E,连结C′E.
(1)求证:四边形ECDC′是菱形;
(2)若BC=CD+AD,试判断四边形ABED的形状,并加以证明.
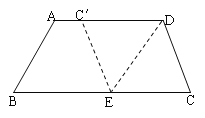
【答案】(1)见解析(2)平行四边形
【解析】
(1)由折叠性质可得CD=C′D,CE=C′E,易证CD=CE,则四边相等,可得四边形CDC′E是菱形;
(2)四边形ABED为平行四边形,由题意易证明AD=BE,又AD∥BC,四边形ABED为平行四边形.
(1)证明:依题意∠C′DE=∠CDE,CD=C′D,CE=C′E,
∵AD∥BC,
∴∠C′DE=∠DEC.
∴∠DEC=∠CDE.
∴CD=CE.
故CD=CE=C′D=C′E,四边形CDC′E是菱形.
(2)解:四边形ABED为平行四边形.
证明:∵BC=CD+AD,又CD=CE,
∴BC=CE+AD.
又BC=CE+BE,
∴AD=BE.
又AD∥BC,可得AD∥BE.
∴四边形ABED为平行四边形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
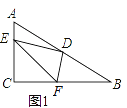
【题目】已知△ABC中,∠ACB=90°,D是AB的中点,∠EDF=90°
(1)如图1,若E、F分别在AC、BC边上,猜想AE2、BF2和EF2之间有何等量关系,并证明你的猜想;
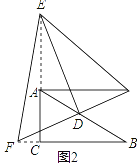
(2)若E、F分别在CA、BC的延长线上,请在图2中画出相应的图形,并判断(1)中的结论是否仍然成立(不作证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O为△ABC的外接圆,AB=AC,直线MN与⊙O相切于点C,弦BD∥MN,AC与BD相交于点E.

(1)求证:△ABE ≌ △ACD;
(2)若AB = 5,BC = 3,求AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
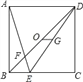
【题目】如图,正方形ABCD中,点E在边BC上,且CE=2BE.连接BD、DE、AE,且AE交BD于F,OG为△BDE的中位线.下列结论:①OG⊥CD;②AB=5OG;③![]() ;④BF=OF;⑤
;④BF=OF;⑤![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P是数轴上表示-2与-1两数的点为端点的线段的中点.
![]()
(1)数轴上点P表示的数为 ;
(2)在数轴上距离点P为2.5个单位长度的点表示的数为 ;
(3)如图,若点P是线段AB(点A在点B的左侧)的中点,且点A表示的数为m,那么点B表示的数是 .(用含m的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究问题:
(1)方法感悟:
如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠BAF=45°,连接EF,求证DE+BF=EF.感悟解题方法,并完成下列填空:将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:AB=AD,BG=DE,∠1=∠2,∠ABG=∠D=90°,∴ ∠ABG+∠ABF=90°+90°=180°,因此,点G,B,F在同一条直线上.
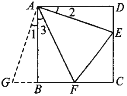
∵ ∠EAF=45°∴ ∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵ ∠1=∠2,∠1+∠3=45°.
即∠GAF=∠________.
又AG=AE,AF=AE
∴ △GAF≌△________.
∴ _________=EF,故DE+BF=EF.
(2)方法迁移:
如图②,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=![]() ∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
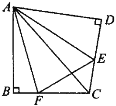
查看答案和解析>>
科目:初中数学 来源: 题型:
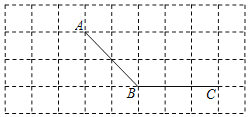
【题目】如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.
![]() 过点C画线段AB的平行线CD;
过点C画线段AB的平行线CD;
![]() 过点A画线段BC的垂线,垂足为E;
过点A画线段BC的垂线,垂足为E;
![]() 过点A画线段AB的垂线,交线段CB的延长线于点F;
过点A画线段AB的垂线,交线段CB的延长线于点F;
![]() 线段AE的长度是点______到直线______的距离;
线段AE的长度是点______到直线______的距离;
![]() 线段AE、BF、AF的大小关系是______
线段AE、BF、AF的大小关系是______![]() 用“
用“![]() ”连接
”连接![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字﹣3,1,3的不透明卡片,它们除数字外都相同,现将它们背面朝上,洗匀后从三张卡片中随机地抽取一张,放回卡片洗匀后,再从三张卡片中随机地抽取一张.
(1)试用列表或画树状图的方法,求两次抽取的卡片上的数字之积为负数的概率;
(2)求两次抽取的卡片上的数字之和为非负数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中有“盈不足术”的问题,原文如下:“今有共买羊,人出五,不足四十五;人出七,不足三.问人数、羊价各几何?”题意是:若干人共同出资买羊,每人出![]() 文,则差
文,则差![]() 文;每人出
文;每人出![]() 文,则差
文,则差![]() 文.
文.
(1)设人数为![]() ,则用含
,则用含![]() 的代数式表示羊价为___________或___________;
的代数式表示羊价为___________或___________;
(2)求人数和羊价各是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com