
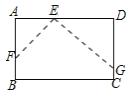
【题目】如图1,在长方形纸片ABCD中,E点在边AD上,F、G分别在边AB、CD上,分别以EF、EG为折痕进行折叠并压平,点A、D的对应点分别是点A′和点D′,若ED′平分∠FEG,且![]() 在
在![]() 内部,如图2,设∠A′ED'=n°,则∠FE D′的度数为___________(用含n的代数式表示).
内部,如图2,设∠A′ED'=n°,则∠FE D′的度数为___________(用含n的代数式表示).
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:
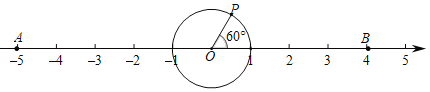
【题目】点A和B在数轴上对应的数分别为a和b,且(a+5)2+|b﹣4|=0.
(1)求线段AB的长;
(2)点C在数轴上所对应的数为x,且x是方程x﹣3=![]() x﹣1的解,在线段BC上是否存在点D,使得AD+BD=
x﹣1的解,在线段BC上是否存在点D,使得AD+BD=![]() CD?若存在,请求出点D在数轴上所对应的数,若不存在,请说明理由;
CD?若存在,请求出点D在数轴上所对应的数,若不存在,请说明理由;
(3)如图,PO=1,点P在AB的上方,且∠POB=60°,点P绕着点O以30度/秒的速度在圆周上顺时针旋转一周停止,同时点Q沿线段AB自点A向点B运动,若P、Q两点能相遇,求点Q的运动速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,每个自然数都有因数,对于一个自然数![]() ,我们把小于
,我们把小于![]() 的正的因数叫做
的正的因数叫做![]() 的真因数.如10的正因数有1、2、5、10,其中1、2、5是10的真因数.把一个自然数
的真因数.如10的正因数有1、2、5、10,其中1、2、5是10的真因数.把一个自然数![]() 的所有真因数的和除以
的所有真因数的和除以![]() ,所得的商叫做
,所得的商叫做![]() 的“完美指标”.如10的“完美指标”是
的“完美指标”.如10的“完美指标”是![]() .一个自然数的“完美指标”越接近1,我们就说这个数越“完美”.如8的“完美指标”是
.一个自然数的“完美指标”越接近1,我们就说这个数越“完美”.如8的“完美指标”是![]() ,10的“完美指标”是
,10的“完美指标”是![]() ,因为
,因为![]() 比5更接近1,所以我们说8比10更完美.
比5更接近1,所以我们说8比10更完美.
(1)试计算5的“完美指标”.
(2)试计算6和9的“完美指标”.
(3)试找出15到20的自然数中,最“完美”的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象经过点A,且点A到x轴的距离是4.
的图象经过点A,且点A到x轴的距离是4.
(1) 求点A的坐标;
(2) 点![]() 为坐标原点,点
为坐标原点,点![]() 是x轴正半轴上一点,当
是x轴正半轴上一点,当![]() 时,求直线AB的解析式.
时,求直线AB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠ACB=90°,D是AB的中点,∠EDF=90°
(1)如图1,若E、F分别在AC、BC边上,猜想AE2、BF2和EF2之间有何等量关系,并证明你的猜想;
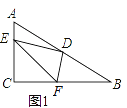
(2)若E、F分别在CA、BC的延长线上,请在图2中画出相应的图形,并判断(1)中的结论是否仍然成立(不作证明)
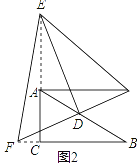
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q.

(1)试证明:无论点P运动到AB上何处时,都有△ADQ≌△ABQ;
(2)当点P在AB上运动到什么位置时,△ADQ的面积是正方形ABCD面积的![]() ;
;
(3)若点P从点A运动到点B,再继续在BC上运动到点C,在整个运动过程中,当点P运动到什么位置时,△ADQ恰为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,已知直线![]() 与x轴、y轴分别交于A、B两点
与x轴、y轴分别交于A、B两点![]() 直线
直线![]() 直线AB于点
直线AB于点![]() 现有一点P从点D出发,沿线段DO向点O运动,另一点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到O时,两点都停止
现有一点P从点D出发,沿线段DO向点O运动,另一点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到O时,两点都停止![]() 设运动时间为t秒.
设运动时间为t秒.![]() 点A的坐标为______;线段OD的长为______.
点A的坐标为______;线段OD的长为______.![]() 设
设![]() 的面积为S,求S与t之间的函数关系
的面积为S,求S与t之间的函数关系![]() 不要求写出取值范围
不要求写出取值范围![]() ,并确定t为何值时S的值最大?
,并确定t为何值时S的值最大?![]() 是否存在某一时刻t,使得
是否存在某一时刻t,使得![]() 为等腰三角形?若存在,写出所有满足条件的t的值;若不存在,则说明理由.
为等腰三角形?若存在,写出所有满足条件的t的值;若不存在,则说明理由.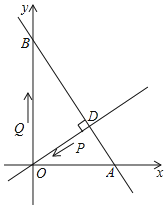
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年春节是市民购买葡萄酒的高峰期,某商场分两批购进同一种葡萄酒,第一批所用资金是8000元,第二批所用资金是10000元.第二批葡萄酒每瓶比第一批葡萄酒每瓶贵90元,结果购买数量比第一批少20%.
(1)求该商场两次共购进多少瓶葡萄酒.
(2)第一批葡萄酒的售价是每瓶200元,很快售完,但因为进价的提高第二批葡萄酒的售价在第一批基础上提高了2a%,实际售卖对比第一批少卖a%,结果两次销售共赚得利润3200元,求a(其中a>25).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究问题:
(1)方法感悟:
如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠BAF=45°,连接EF,求证DE+BF=EF.感悟解题方法,并完成下列填空:将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:AB=AD,BG=DE,∠1=∠2,∠ABG=∠D=90°,∴ ∠ABG+∠ABF=90°+90°=180°,因此,点G,B,F在同一条直线上.
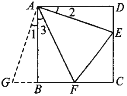
∵ ∠EAF=45°∴ ∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵ ∠1=∠2,∠1+∠3=45°.
即∠GAF=∠________.
又AG=AE,AF=AE
∴ △GAF≌△________.
∴ _________=EF,故DE+BF=EF.
(2)方法迁移:
如图②,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=![]() ∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
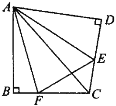
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com