
【题目】请在下列两题中选取一题解答:
(1)已知a是方程 ![]() 的解,求代数式(a﹣1)2﹣a(a﹣3)的值;
的解,求代数式(a﹣1)2﹣a(a﹣3)的值;
(2)化简: ![]() ,在不等式x≤2的非负整数解中选择一个适当的数代入求值.
,在不等式x≤2的非负整数解中选择一个适当的数代入求值.
【答案】
(1)
解: ![]() ,
,
去分母2=a+1,
a=1,
经检验a=1是原方程的解
原式=a2﹣2a+1-a2+3a
=a+1
=2
(2)![]()
解: 原式= ![]()
= ![]()
当x=1时,原式= ![]()
【解析】(1)解分式方程,求出a的值,代入题中代数式求值即可;
(2)把分式化成最简形式,然后在x≤2的非负整数解中知x=0, 1, 2,但要保证分式有意义,x不能取0,2,把x=1代入代数式即可.
【考点精析】解答此题的关键在于理解去分母法的相关知识,掌握先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊,以及对代数式求值的理解,了解求代数式的值,一般是先将代数式化简,然后再将字母的取值代入;求代数式的值,有时求不出其字母的值,需要利用技巧,“整体”代入.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知点A(﹣1,0),点B(0,2),点C(3,0),直线a为过点D(0,﹣1)且平行于x轴的直线. 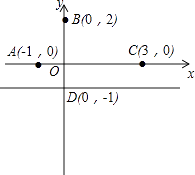
(1)直接写出点B关于直线a对称的点E的坐标;
(2)若P为直线a上一动点,请求出△PBA周长的最小值和此时P点坐标;
(3)若M为直线a上一动点,且S△ABC=S△MAB , 请求出M点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.90°的角叫余角
B.一个角的补角一定是钝角
C.如果两个角互补,其中一个是钝角,那么另一个角一定是锐角
D.已知∠A+∠B+∠C=180°,则∠A、∠B、∠C互补
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动手操作题:如何能把一个三角形分成两个等腰三角形吗?
实际上,一个三角形只要具备下列三个条件之一,都可以被分成两个等腰三角形:
①一个角为90°;②一个角是另一个的2倍(第三角必须大于45°);
③一个角是另一个角的3倍.今天,我们通过作图来验证这个结论。
(1)问题1:
如图,Rt△ABC中,求画一条直线l将△ABC分成两个等腰三角形.并说明直线l与△ABC
边上的交点D的位置.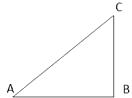
(2)问题2:
如图,△ABC中,∠ACB=80°, ∠BAC=40°,求画一条直线l把△ABC分成两个等腰三角形, 并在图中标注两个顶角的度数.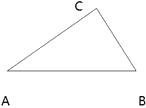
(3)问题3:
如图,△ABC中,∠ACB=120°, ∠BAC=40°,求画一条直线l把△ABC分成两个等腰三角形, 并在图中标注两个顶角的度数.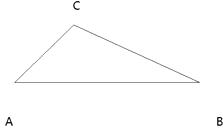
(4)问题:4:
如果等腰三角形能被一条直线分成两个等腰三角形,则原等腰三角形的顶角可以是°.(至少写出三个)
(5)拓展:已知△ABC的三条边长分别为3,4,6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )
A.6条
B.7条
C.8条
D.9条
查看答案和解析>>
科目:初中数学 来源: 题型:
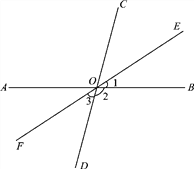
【题目】如图,直线AB、CD相交于点O,∠BOC=80°,OE是∠BOC的角平分线,OF是OE的反向延长线.
(1)求∠2、∠3的度数;
(2)说明OF平分∠AOD的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是随机事件的是( )
A. 每周有7天
B. 袋中有三个红球,摸出一个球一定是红球
C. 在同一平面内,垂直于同一条直线的两条直线互相垂直
D. 任意购买一张车票,座位刚好靠窗口
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com