
【题目】如图,在平面直角坐标系xOy中,已知点A(﹣1,0),点B(0,2),点C(3,0),直线a为过点D(0,﹣1)且平行于x轴的直线. 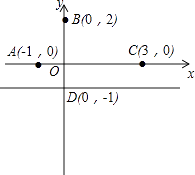
(1)直接写出点B关于直线a对称的点E的坐标;
(2)若P为直线a上一动点,请求出△PBA周长的最小值和此时P点坐标;
(3)若M为直线a上一动点,且S△ABC=S△MAB , 请求出M点坐标.
【答案】
(1)(0,﹣4)
(2)解:∵B、E关于直线a对称,
∴PB=PE,
∴△PBA周长=AB+BP+PA
=AB+PE+PA
∵两点之间线段最段,
∴△PBA周长的最小值=AB+AE= ![]() ,
,
∴直线AE的解析式:y=﹣4x﹣4,
当y=﹣1时,x= ![]() ,
,
∴P点坐标( ![]() ,﹣1)
,﹣1)
(3)解:设M(m,﹣1),
当M在第四象限,
∵S△ABC=S△MAB,
∴点M在过C且平行于AB的直线上,
∵直线AB的解析式为:y=2x+2,
设直线CM的解析式为:y=2x+n,
∴0=2×3+n,
∴n=﹣6,
∴直线CM的解析式为:y=2x﹣6,
∴m= ![]() ,
,
∴M( ![]() ,﹣1),
,﹣1),
当M在第三象限,
直线AB与直线a交于G(﹣ ![]() ,﹣1),
,﹣1),
∴ ![]() ×(﹣
×(﹣ ![]() ﹣m)×(2+1)﹣
﹣m)×(2+1)﹣ ![]() ×(﹣
×(﹣ ![]() ﹣m)×1=
﹣m)×1= ![]() ×4×2,
×4×2,
∴m=﹣5.5,
∴M(﹣5.5,﹣1).

【解析】解:(1)∵B(0,2),D(0,﹣1), ∴BD=3,
∵直线a为过点D(0,﹣1)且平行于x轴的直线.
∴BD⊥直线a,
∴点B关于直线a对称的点E的坐标(0,﹣4);
所以答案是:(0,﹣4);
【考点精析】利用轴对称-最短路线问题对题目进行判断即可得到答案,需要熟知已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】已知一个由50个偶数排成的数阵.用如图所示的框去框住四个数,并求出这四个数的和.在下列给出备选答案中,有可能是这四个数的和的是( )
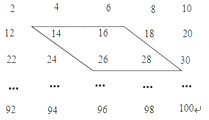
A. 80 B. 172
C. 148 D. 220
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年9月3日在北京举行的中国人民抗日战争暨世界反法西斯战争胜利70周年阅兵活动中,12000名将士接受了党和人民的检阅,将12000用科学记数法表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
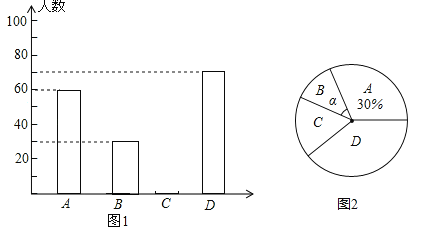
【题目】黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:
(1)本次抽样调查共抽取了多少名学生?并将条形统计图补充完整;
(2)本次抽样调查中,学习时间的中位数落在哪个等级内?
(3)表示B等级的扇形圆心角α的度数是多少?
(4)在此次问卷调查中,甲班有2人平均每天课外学习时间超过2小时,乙班有3人平均每天课外学习时间超过2小时,若从这5人中任选2人去参加座谈,试用列表或化树状图的方法求选出的2人来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第(n+1)个三角形以 ![]() 为顶点的内角的度数是( )
为顶点的内角的度数是( )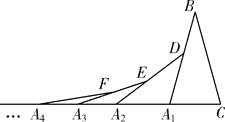
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请在下列两题中选取一题解答:
(1)已知a是方程 ![]() 的解,求代数式(a﹣1)2﹣a(a﹣3)的值;
的解,求代数式(a﹣1)2﹣a(a﹣3)的值;
(2)化简: ![]() ,在不等式x≤2的非负整数解中选择一个适当的数代入求值.
,在不等式x≤2的非负整数解中选择一个适当的数代入求值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com