
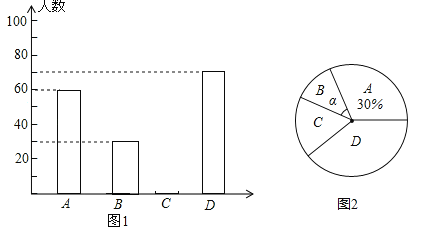
【题目】黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:
(1)本次抽样调查共抽取了多少名学生?并将条形统计图补充完整;
(2)本次抽样调查中,学习时间的中位数落在哪个等级内?
(3)表示B等级的扇形圆心角α的度数是多少?
(4)在此次问卷调查中,甲班有2人平均每天课外学习时间超过2小时,乙班有3人平均每天课外学习时间超过2小时,若从这5人中任选2人去参加座谈,试用列表或化树状图的方法求选出的2人来自不同班级的概率.
【答案】(1)200;(2)C;(3)54°;(4)![]() .
.
【解析】
试题分析:(1)根据B类的人数和所占的百分比即可求出总数;求出C的人数从而补全统计图;
(2)根据中位数定义:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数可得答案;
(3)用B的人数除以总人数再乘以360°,即可得到圆心角α的度数;
(4)先设甲班学生为A1,A2,乙班学生为B1,B2,B3根据题意画出树形图,再根据概率公式列式计算即可.
试题解析:(1)共调查的中学生数是:80÷40%=200(人),C类的人数是:200﹣60﹣80﹣20=40(人),如图1:

(2)本次抽样调查中,学习时间的中位数落在C等级内;
(3)根据题意得:α=![]() ×360°=54°;
×360°=54°;
(4)设甲班学生为A1,A2,乙班学生为B1,B2,B3,画树状图为:
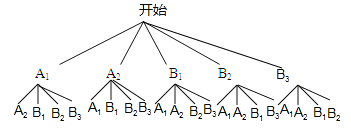
一共有20种等可能结果,其中2人来自不同班级共有12种,∴P(2人来自不同班级)=![]() =
=![]() .
.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:初中数学 来源: 题型:
【题目】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( ) 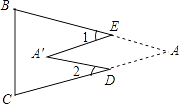
A.∠A=∠1+∠2
B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2
D.3∠A=2(∠1+∠2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD是平行四边形,AC、BD交于点O,∠1=∠2.
(1)求证:四边形ABCD是矩形;
(2)若∠BOC=120°,AB=4cm,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个全等的△ABC和△DEF重叠在一起,固定△ABC,将△DEF进行如下变换:
(1)如图1,△DEF沿直线CB向右平移(即点F在线段CB上移动),连接AF、AD、BD,请直接写出S△ABC与S四边形AFBD的关系
(2)如图2,当点F平移到线段BC的中点时,若四边形AFBD为正方形,那么△ABC应满足什么条件:请给出证明;
(3)在(2)的条件下,将△DEF沿DF折叠,点E落在FA的延长线上的点G处,连接CG,请你画出图形,此时CG与CF有何数量关系.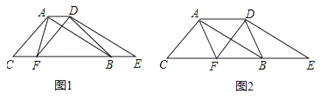
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A.C的坐标分别为(10,0),(0,3),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为 . 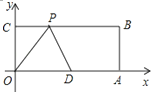
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验室里,水平桌面上有甲、乙两个圆柱形容器(容器足够高),底面半径之比为1∶2,用一个管子在甲、乙两个容器的15厘米高度处连通(即管子底端离容器底15厘米).已知只有乙容器中有水,水位高2厘米,如图所示.现同时向甲、乙两个容器注水,平均每分钟注入乙容器的水量是注入甲容器水量的k倍.开始注水1分钟,甲容器的水位上升a厘米,且比乙容器的水位低1厘米.其中a,k均为正整数,当甲、乙两个容器的水位都到达连通管子的位置时,停止注水.甲容器的水位有2次比乙容器的水位高1厘米,设注水时间为t分钟.

(1)求k的值(用含a的代数式表示).
(2)当甲容器的水位第一次比乙容器的水位高1厘米时,求t的值.
(3)当甲容器的水位第二次比乙容器的水位高1厘米时,求a,k,t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com