
����Ŀ����ͼ������ȫ�ȵġ�ABC�͡�DEF�ص���һ�𣬹̶���ABC������DEF�������±任��
��1����ͼ1����DEF��ֱ��CB����ƽ�ƣ�����F���߶�CB���ƶ���������AF��AD��BD����ֱ��д��S��ABC��S�ı���AFBD�Ĺ�ϵ
��2����ͼ2������Fƽ�Ƶ��߶�BC���е�ʱ�����ı���AFBDΪ�����Σ���ô��ABCӦ����ʲô�����������֤����
��3���ڣ�2���������£�����DEF��DF�۵�����E����FA���ӳ����ϵĵ�G��������CG�����㻭��ͼ�Σ���ʱCG��CF�к�������ϵ��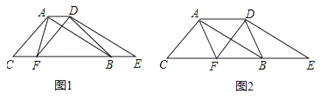
���𰸡��⣺��1��S��ABC=S�ı���AFBD ��
���ɣ�������ɵã�AD��EC��
��S��ADF=S��ABD ��
��S��ACF=S��ADF=S��ABD ��
��S��ABC=S�ı���AFBD��
��2����ABCΪ����ֱ�������Σ�����AB=AC����BAC=90�㣬
�������£�
��FΪBC���е㣬
��CF=BF��
��CF=AD��
��AD=BF��
�֡�AD��BF��
���ı���AFBDΪƽ���ı��Σ�
��AB=AC��FΪBC���е㣬
��AF��BC��
��ƽ���ı���AFBDΪ����
�ߡ�BAC=90�㣬FΪBC���е㣬
��AF=![]() BC=BF��
BC=BF��
���ı���AFBDΪ�����Σ�
��3����ͼ3��ʾ��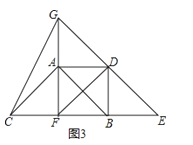
�ɣ�2��֪����ABCΪ����ֱ�������Σ�AF��BC��
��CF=k����GF=EF=CB=2k��
�ɹ��ɶ����ã�CG=![]() k��
k��
��CG=![]() CF��
CF��
����������1������ƽ���ߵ������Լ������������ϵ���ó��𰸣�
��2������ƽ���ı��ε��ж��ó��ı���AFBDΪƽ���ı��Σ������ó�AF=![]() BC=BF������𰸣�
BC=BF������𰸣�
��3���������⻭��ͼ�Σ���CF=k�����ù��ɶ���������ɣ�
�����㾫�������ڱ��⿼���ƽ���ߵ����ʺ��ɶ����ĸ����Ҫ�˽���ֱ��ƽ�У�ͬλ����ȣ���ֱ��ƽ�У��ڴ�����ȣ���ֱ��ƽ�У�ͬ���ڽǻ�����ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2���ܵó���ȷ�𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ѡ�ABCֽƬ��DE�۵�������A�����ı���BCDE�ڲ�ʱ�����A���1+��2֮����һ��������ϵʼ�ձ��ֲ��䣬��������һ��������ɣ���������ǣ� ��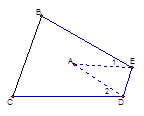
A.��A=��1+��2
B.2��A=��1+��2
C.3��A=2��1+��2
D.3��A=2����1+��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����x2-81=0����ôx2-81=0���������ֱ���x1=________��x2=__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʯīϩ(Graphene)�Ǵ�ʯī�����а����������̼ԭ����ɵ�ֻ��һ��ԭ�Ӻ�ȵĶ�ά���壮ʯīϩһ������������ʯī����1����ʯī��Լ����300���ʯīϩ��300���ÿ�ѧ��������ʾΪ(����)
A. 3��106 B. 30��105 C. 300��104 D. 3000000
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
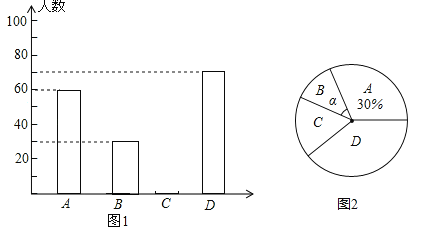
����Ŀ��ǭ������ij��ѧΪ�˽ⱾУѧ��ƽ��ÿ��Ŀ���ѧϰʵ������������ȡ����ѧ�������ʾ����飬������������ΪA��B��C��D�ĸ��ȼ�����ѧ��ʱ��Ϊt��Сʱ����A��t��1��B��1��t��1.5��C��1.5��t��2��D��t��2�����ݵ�������������ͼ��ʾ��������������ͳ��ͼ���������ͼ����Ϣ����������⣺
��1�����γ������鹲��ȡ�˶�����ѧ������������ͳ��ͼ����������
��2�����γ��������У�ѧϰʱ�����λ�������ĸ��ȼ��ڣ�
��3����ʾB�ȼ�������Բ�ĽǦ��Ķ����Ƕ��٣�
��4���ڴ˴��ʾ������У��װ���2��ƽ��ÿ�����ѧϰʱ�䳬��2Сʱ���Ұ���3��ƽ��ÿ�����ѧϰʱ�䳬��2Сʱ��������5������ѡ2��ȥ�μ���̸�������б�����״ͼ�ķ�����ѡ����2�����Բ�ͬ�༶�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʹ����ʽ������x��ȡֵ��Χ��
��x��1��3����x��1����x2��2x+3����0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ѷ���ʽ��x��2��2��4x+8��ʽ�ֽʼ���ִ����һ����__
�⣺ԭʽ=��x��2��2����4x��8����A
=��x��2��2��4��x��2����B
=��x��2����x��2+4����C
=��x��2����x+2����D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
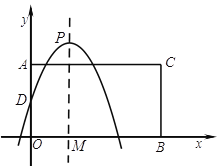
����Ŀ����ͼ, ��ƽ��ֱ������ϵ��,��A��B�ֱ���![]() ��������,
��������, ![]() ����������������,
����������������, ![]() ��
�� ![]() ����AO��BOΪ�ڱ߹������AOBC��������
����AO��BOΪ�ڱ߹������AOBC��������![]() ��
��![]() ���ڵ�D��PΪ���㣬PM��
���ڵ�D��PΪ���㣬PM��![]() ���ڵ�M��
���ڵ�M��
��1����![]() ��
�� ![]() �ij�(������ú�
�ij�(������ú�![]() �Ĵ���ʽ��ʾ)��
�Ĵ���ʽ��ʾ)��
��2����![]() ʱ,��������ߵı���ʽ��
ʱ,��������ߵı���ʽ��
��3���ڵ�![]() �������˶������У�
�������˶������У�
��������![]() �ǵ���������,�������������������
�ǵ���������,�������������������![]() ��ֵ��
��ֵ��
�ڵ���A����ֱ��DP�ĶԳƵ�![]() ǡ������������
ǡ������������![]() ��ͼ����ʱ����ֱ��д��
��ͼ����ʱ����ֱ��д��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com