
����Ŀ����ͼ, ��ƽ��ֱ������ϵ��,��A��B�ֱ���![]() ��������,
��������, ![]() ����������������,
����������������, ![]() ��
�� ![]() ����AO��BOΪ�ڱ߹������AOBC��������
����AO��BOΪ�ڱ߹������AOBC��������![]() ��
��![]() ���ڵ�D��PΪ���㣬PM��
���ڵ�D��PΪ���㣬PM��![]() ���ڵ�M��
���ڵ�M��
��1����![]() ��
�� ![]() �ij�(������ú�
�ij�(������ú�![]() �Ĵ���ʽ��ʾ)��
�Ĵ���ʽ��ʾ)��
��2����![]() ʱ,��������ߵı���ʽ��
ʱ,��������ߵı���ʽ��
��3���ڵ�![]() �������˶������У�
�������˶������У�
��������![]() �ǵ���������,�������������������
�ǵ���������,�������������������![]() ��ֵ��
��ֵ��
�ڵ���A����ֱ��DP�ĶԳƵ�![]() ǡ������������
ǡ������������![]() ��ͼ����ʱ����ֱ��д��
��ͼ����ʱ����ֱ��д��![]() ��ֵ��
��ֵ��
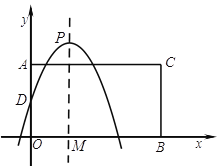
���𰸡���1��OD��Ϊk��PM�ij�Ϊk+3��
��2���������ߵı���ʽΪ![]() ��
��
��3��������������![]() ��ֵΪ
��ֵΪ![]() �� 6����
�� 6����![]()
��![]() ��ֵΪ
��ֵΪ![]() .
.
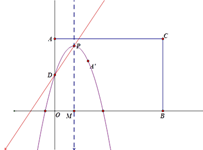
����������1����D��y=��x2+3x+k�ϣ�����y���ϣ���y=0�����D���꣬���������߶��㹫ʽ��������ɣ�
��2������k��ʾ����صĵ�����꣬����PM=BM�������̼��ɣ�
��3��������k��ʾ����صĵ�����꣬���ݡ�ADP�ǵ��������Σ������������AD=AP��DA=DP��PA=PD���㣻
���ɵ�P��D�������ֱ��PD����ʽ������PD��AA�䣬��A��0��2k����ȷ����AA�����ʽ���̶�������㣬�����A������꼴�ɣ�
�⣺��1����x=0������![]() ����
����![]() ����
����![]() ��
��
��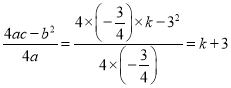 ����
����![]() ��
��
��2����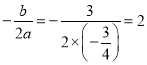 ����
����![]() ,
, ![]() ��
��
�֡�![]() ��
�� ![]() ����
����![]() �����
�����![]() ��
��
��������ߵı���ʽΪ![]() ��
��
��3����
����P�ھ���AOBC�ⲿʱ
��ͼ��ʾ��
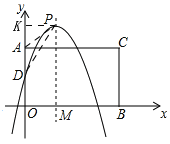
��P��PK��OA�ڵ�K����AD=APʱ,
��AD=AO-DO=2k-k=k��
��AD=AP =k��KA=KO-AO=PM-AO= ![]()
KP=OM=2����Rt��KAP�� ![]()
��![]() �����
�����![]() ��
��
����P�ھ���AOBC�ڲ�ʱ
��PD=APʱ,��ͼ��ʾ��

��P��PH��OA��H��
AD=k��HD=![]() ��
�� ![]()
�֡�HO=PM= ![]() ��
��
��![]() �����
�����![]() ��
��
��DP=DAʱ,��ͼ��ʾ��

��D��PQ��PM��Q��
PQ=PM-QM=PM-OD= ![]()
DQ=OM=2��DP=DA=k��
��Rt��DQP�� ![]() ��
��
��![]() ��
��
��![]() ��
��
���㾦�������Ƕ��κ����ۺ��⣬��Ҫ�����˶��κ�������ʽ��ȷ����ƽ������ϵ�����߶εij������������ε����ʣ�ȷ������������ʽ�ǽⱾ��Ĺؼ�. �⣨3���DZ�����ѵ�.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ȫ�ȵġ�ABC�͡�DEF�ص���һ�𣬹̶���ABC������DEF�������±任��
��1����ͼ1����DEF��ֱ��CB����ƽ�ƣ�����F���߶�CB���ƶ���������AF��AD��BD����ֱ��д��S��ABC��S�ı���AFBD�Ĺ�ϵ
��2����ͼ2������Fƽ�Ƶ��߶�BC���е�ʱ�����ı���AFBDΪ�����Σ���ô��ABCӦ����ʲô�����������֤����
��3���ڣ�2���������£�����DEF��DF�۵�����E����FA���ӳ����ϵĵ�G��������CG�����㻭��ͼ�Σ���ʱCG��CF�к�������ϵ��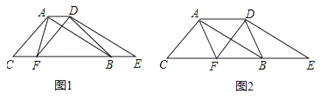
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x2��8x+15=0������ɺ���x����ȫƽ����ʽ��������ȷ���ǣ� ��
A. x2��8x+����4��2=31 B. x2��8x+����4��2=1
C. x2+8x+42=1 D. x2��4x+4=��11
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ��̽����
��1�����ֲ�����
����ͼ1����һ��ֱ�����ǰ�DEF������ֱ�����ǰ�ABC�ϣ�ʹ���ǰ�DEF������ֱ�DZ�DE��DF�ֱ���B��C����BC��EF����֪��A=30�㣬���ABD+��ACD=��
����ͼ2����ֱ�����ǰ�ABC�������ı����ֱ�����ǰ�DEF��λ�ã�ʹ���ǰ�DEF������ֱ�DZ�DE��DF��Ȼ�ֱ���B��C����ô��ABD+��ACD= 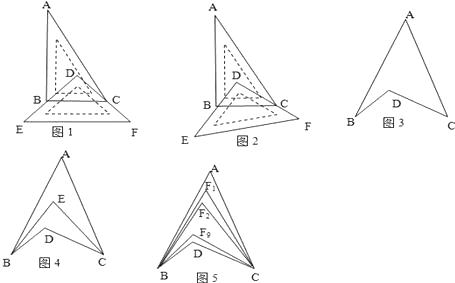
��2������֤����
��ͼ3����BDC���A����B����C֮�������ʲô��ϵ����˵�����ɣ�
��3�����Ӧ�ã�
����ֱ���������Ͻ��ۣ�������������⣺
����ͼ4��BEƽ�֡�ABD��CEƽ�֡�ACB������BAC=40�㣬��BDC=120�㣬���BEC�Ķ�����
��4������ͼ5����ABD����ACD��10�ȷ����ཻ�ڵ�F1��F2������F9 ��
����BDC=120�㣬��BF3C=64�㣬���A�Ķ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ȥ�Ϫ��ij���㴺�Σ�����������ѧ���Ƴ����շѱ����£�
����m | 0��m��100 | 100��m��200 | m��200 |
�շѱ���Ԫ/�ˣ� | 90 | 80 | 70 |
��֪��У���꼶�μӴ���ѧ����������100�ˣ����꼶�μӴ���ѧ����������100�ˣ������㣬�������꼶�ֱ����Ź��軨��17700Ԫ���������꼶��������ֻ�軨��14700Ԫ��
��1�������꼶�μӴ���ѧ������֮�ͳ���200����Ϊʲô��
��2�������꼶�μӴ���ѧ�����ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ�����ˮƽ�������мס�������Բ���������������㹻�ߣ�������뾶֮��Ϊ1��2����һ�������ڼס�������������15���߶ȴ���ͨ�������ӵ���������15���ף�����ֻ֪������������ˮ��ˮλ��2���ף���ͼ��ʾ����ͬʱ��ס�����������עˮ��ƽ��ÿ����ע����������ˮ����ע�������ˮ����k������ʼעˮ1���ӣ���������ˮλ����a���ף��ұ���������ˮλ��1���ף�����a��k��Ϊ�����������ס�������������ˮλ��������ͨ���ӵ�λ��ʱ��ֹͣעˮ����������ˮλ��2�α���������ˮλ��1���ף���עˮʱ��Ϊt���ӣ�

��1����k��ֵ���ú�a�Ĵ���ʽ��ʾ����
��2������������ˮλ��һ�α���������ˮλ��1����ʱ����t��ֵ��
��3������������ˮλ�ڶ��α���������ˮλ��1����ʱ����a��k��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������a��b�Ķ���ʽ2��a2��2ab��b2������a2+mab+2b2������ab���m= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c��d��������0������![]() �� ���ݷ�ʽ�Ļ������ʡ���ʽ�Ļ������ʼ����㷨��̽����������е�������ʽ֮����ʲô��ϵ��Ȼ��ѡ������һ����о���˵����
�� ���ݷ�ʽ�Ļ������ʡ���ʽ�Ļ������ʼ����㷨��̽����������е�������ʽ֮����ʲô��ϵ��Ȼ��ѡ������һ����о���˵����
��1��![]() ��
��![]() �� ��2��
�� ��2��![]() ��
��![]() �� ��3��
�� ��3��![]() ��
��![]() ��a��b��c��d����
��a��b��c��d����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com