
【题目】实验探究:
(1)动手操作:
①如图1,将一块直角三角板DEF放置在直角三角板ABC上,使三角板DEF的两条直角边DE、DF分别经过点B、C,且BC∥EF,已知∠A=30°,则∠ABD+∠ACD=;
②如图2,若直角三角板ABC不动,改变等腰直角三角板DEF的位置,使三角板DEF的两条直角边DE、DF仍然分别经过点B、C,那么∠ABD+∠ACD= 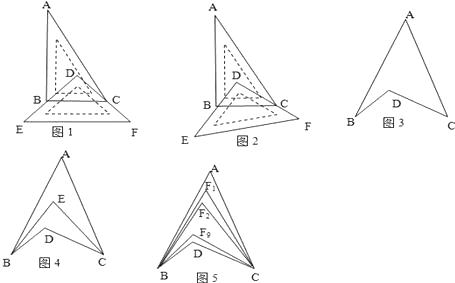
(2)猜想证明:
如图3,∠BDC与∠A、∠B、∠C之间存在着什么关系,并说明理由;
(3)灵活应用:
请你直接利用以上结论,解决以下列问题:
①如图4,BE平分∠ABD,CE平分∠ACB,若∠BAC=40°,∠BDC=120°,求∠BEC的度数;
(4)②如图5,∠ABD,∠ACD的10等分线相交于点F1、F2、…、F9 ,
若∠BDC=120°,∠BF3C=64°,则∠A的度数为 .
【答案】
(1)60°;60°
(2)
猜想:∠A+∠B+∠C=∠BDC;
证明:连接BC,
在△DBC中,∵∠DBC+∠DCB+∠D=180°,
∴∠DBC+∠DCB=180°﹣∠BDC;
在Rt△ABC中,
∵∠ABC+∠ACB+∠A=180°,
即∠ABD+∠DBC+∠DCB+∠ACD+∠A=180°,
而∠DBC+∠DCB=180°﹣∠BDC,
∴∠A+∠ABD+∠ACD=180°﹣=∠BDC,
即:∠A+∠B+∠C=∠BDC
(3)
①由(2)可知∠A+∠ABD+∠ACD=∠BDC,∠A+∠ABE+∠ACE=∠BEC,
∵∠BAC=40°,∠BDC=120°,
∴∠ABD+∠ACD=120°﹣40°=80°
∵BE平分∠ABD,CE平分∠ACB,
∴∠ABE+∠ACE=40°,
∴∠BEC=40°+40°=80°;
(4)40°
【解析】解:(1)动手操作:
①∵BC∥EF,
∴∠DBC=∠E=∠F=∠DCB=45°,
∴∠ABD=90°﹣45°=45°,∠ACD=60°﹣45°=15°,
∴∠ABD+∠ACD=60°;
②在△DBC中,∵∠DBC+∠DCB+∠D=180°,
而∠D=90°,
∴∠DBC+∠DCB=90°;
在Rt△ABC中,
∵∠ABC+∠ACB+∠A=180°,
即∠ABD+∠DBC+∠DCB+∠ACD+∠A=180°,
而∠DBC+∠DCB=90°,
∴∠ABD+∠ACD=90°﹣∠A=60°.
所以答案是60°;60°;
4)②由(2)可知:∠A+∠ABD+∠ACD=∠BDC=120°,∠ABF3+∠ACF3=∠BF3C=64°,
∵∠ABF3= ![]() ∠ABD,∠ACF3=
∠ABD,∠ACF3= ![]() ∠ACD,
∠ACD,
∴ABD+∠ACD=120°﹣∠A,∠A+ ![]() (∠ABD+∠ACD)=64°,
(∠ABD+∠ACD)=64°,
∴∠A+ ![]() =64°,
=64°,
∴∠A=40°,
所以答案是40°.
【考点精析】掌握三角形的内角和外角是解答本题的根本,需要知道三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】把多项式(x﹣2)2﹣4x+8因式分解开始出现错误的一步是__
解:原式=(x﹣2)2﹣(4x﹣8)…A
=(x﹣2)2﹣4(x﹣2)…B
=(x﹣2)(x﹣2+4)…C
=(x﹣2)(x+2)…D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在平面直角坐标系中,点A,B分别是![]() 轴正半轴,
轴正半轴, ![]() 轴正半轴上两动点,
轴正半轴上两动点, ![]() ,
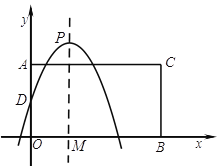
, ![]() ,以AO,BO为邻边构造矩形AOBC,抛物线
,以AO,BO为邻边构造矩形AOBC,抛物线![]() 交
交![]() 轴于点D,P为顶点,PM⊥
轴于点D,P为顶点,PM⊥![]() 轴于点M.
轴于点M.
(1)求![]() ,
, ![]() 的长(结果均用含
的长(结果均用含![]() 的代数式表示).
的代数式表示).
(2)当![]() 时,求该抛物线的表达式.
时,求该抛物线的表达式.
(3)在点![]() 在整个运动过程中.
在整个运动过程中.
①若存在![]() 是等腰三角形,请求出所有满足条件的
是等腰三角形,请求出所有满足条件的![]() 的值.
的值.
②当点A关于直线DP的对称点![]() 恰好落在抛物线
恰好落在抛物线![]() 的图象上时,请直接写出
的图象上时,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD、BE分别是△ABC的中线,AD、BE相交于点F. 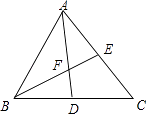
(1)△ABC与△ABD的面积有怎样的数量关系?为什么?
(2)△BDF与△AEF的面积有怎样的数量关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“新禧”杂货店去批发市场购买某种新型儿童玩具,第一次用1200元购得玩具若干个,并以7元的价格出售,很快就售完.由于该玩具深受儿童喜爱,第二次进货时每个玩具的批发价已比第一次提高了20%,他用1500元所购买的玩具数量比第一次多10个,再按8元售完,问该老板两次一共赚了多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com