
【题目】如图1,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形,E是AB的中点,连接CE并延长交AD于F. 
(1)求证:①△AEF≌△BEC;②四边形BCFD是平行四边形;
(2)如图2,将四边形ACBD折叠,使D与C重合,HK为折痕,求sin∠ACH的值.
【答案】
(1)
证明:①在△ABC中,∠ACB=90°,∠CAB=30°,
∴∠ABC=60°.
在等边△ABD中,∠BAD=60°,
∴∠BAD=∠ABC=60°.
∵E为AB的中点,
∴AE=BE.
又∵∠AEF=∠BEC,
∴△AEF≌△BEC.
②在△ABC中,∠ACB=90°,E为AB的中点,
∴CE= ![]() AB,BE=
AB,BE= ![]() AB.
AB.
∴CE=AE,
∴∠EAC=∠ECA=30°,
∴∠BCE=∠EBC=60°.
又∵△AEF≌△BEC,
∴∠AFE=∠BCE=60°.
又∵∠D=60°,
∴∠AFE=∠D=60°.
∴FC∥BD.
又∵∠BAD=∠ABC=60°,
∴AD∥BC,即FD∥BC.
∴四边形BCFD是平行四边形
;
证明:①在△ABC中,∠ACB=90°,∠CAB=30°,
∴∠ABC=60°.
在等边△ABD中,∠BAD=60°,
∴∠BAD=∠ABC=60°.
∵E为AB的中点,
∴AE=BE.
又∵∠AEF=∠BEC,
∴△AEF≌△BEC.
②在△ABC中,∠ACB=90°,E为AB的中点,
∴CE= ![]() AB,BE=
AB,BE= ![]() AB.
AB.
∴CE=AE,
∴∠EAC=∠ECA=30°,
∴∠BCE=∠EBC=60°.
又∵△AEF≌△BEC,
∴∠AFE=∠BCE=60°.
又∵∠D=60°,
∴∠AFE=∠D=60°.
∴FC∥BD.
又∵∠BAD=∠ABC=60°,
∴AD∥BC,即FD∥BC.
∴四边形BCFD是平行四边形
;证明:①在△ABC中,∠ACB=90°,∠CAB=30°,
∴∠ABC=60°.
在等边△ABD中,∠BAD=60°,
∴∠BAD=∠ABC=60°.
∵E为AB的中点,
∴AE=BE.
又∵∠AEF=∠BEC,
∴△AEF≌△BEC.
②在△ABC中,∠ACB=90°,E为AB的中点,
∴CE= ![]() AB,BE=
AB,BE= ![]() AB.
AB.
∴CE=AE,
∴∠EAC=∠ECA=30°,
∴∠BCE=∠EBC=60°.
又∵△AEF≌△BEC,
∴∠AFE=∠BCE=60°.
又∵∠D=60°,
∴∠AFE=∠D=60°.
∴FC∥BD.
又∵∠BAD=∠ABC=60°,
∴AD∥BC,即FD∥BC.
∴四边形BCFD是平行四边形
(2)
解:∵∠BAD=60°,∠CAB=30°,
∴∠CAH=90°.
在Rt△ABC中,∠CAB=30°,设BC=a,
∴AB=2BC=2a.
∴AD=AB=2a.
设AH=x,则HC=HD=AD﹣AH=2a﹣x,
在Rt△ABC中,AC2=(2a)2﹣a2=3a2,
在Rt△ACH中,AH2+AC2=HC2,即x2+3a2=(2a﹣x)2,
解得x= ![]() a,即AH=
a,即AH= ![]() a.∴HC=2a﹣x=2a﹣
a.∴HC=2a﹣x=2a﹣ ![]() a=
a= ![]() a.∴sin∠ACH=
a.∴sin∠ACH= 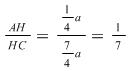 .
.
;
解:∵∠BAD=60°,∠CAB=30°,
∴∠CAH=90°.
在Rt△ABC中,∠CAB=30°,设BC=a,
∴AB=2BC=2a.
∴AD=AB=2a.
设AH=x,则HC=HD=AD﹣AH=2a﹣x,
在Rt△ABC中,AC2=(2a)2﹣a2=3a2,
在Rt△ACH中,AH2+AC2=HC2,即x2+3a2=(2a﹣x)2,
解得x= ![]() a,即AH=
a,即AH= ![]() a.∴HC=2a﹣x=2a﹣
a.∴HC=2a﹣x=2a﹣ ![]() a=
a= ![]() a.∴sin∠ACH=
a.∴sin∠ACH= 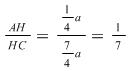 .
.
;解:∵∠BAD=60°,∠CAB=30°,
∴∠CAH=90°.
在Rt△ABC中,∠CAB=30°,设BC=a,
∴AB=2BC=2a.
∴AD=AB=2a.
设AH=x,则HC=HD=AD﹣AH=2a﹣x,
在Rt△ABC中,AC2=(2a)2﹣a2=3a2,
在Rt△ACH中,AH2+AC2=HC2,即x2+3a2=(2a﹣x)2,
解得x= ![]() a,即AH=
a,即AH= ![]() a.∴HC=2a﹣x=2a﹣
a.∴HC=2a﹣x=2a﹣ ![]() a=
a= ![]() a.∴sin∠ACH=
a.∴sin∠ACH= 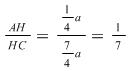 .
.
【解析】(1)①在△ABC中,由已知可得∠ABC=60°,从而推得∠BAD=∠ABC=60°.由E为AB的中点,得到AE=BE.又因为∠AEF=∠BEC,所以△AEF≌△BEC.②在Rt△ABC中,E为AB的中点,则CE= ![]() AB,BE=
AB,BE= ![]() AB,得到∠BCE=∠EBC=60°.由△AEF≌△BEC,得∠AFE=∠BCE=60°.又∠D=60°,得∠AFE=∠D=60度.所以FC∥BD,又因为∠BAD=∠ABC=60°,所以AD∥BC,即FD∥BC,则四边形BCFD是平行四边形.(2)在Rt△ABC中,设BC=a,则AB=2BC=2a,AD=AB=2a.设AH=x,则HC=HD=AD﹣AH=2a﹣x.在Rt△ABC中,由勾股定理得AC2=3a2 . 在Rt△ACH中,由勾股定理得AH2+AC2=HC2 , 即x2+3a2=(2a﹣x)2 . 解得x=
AB,得到∠BCE=∠EBC=60°.由△AEF≌△BEC,得∠AFE=∠BCE=60°.又∠D=60°,得∠AFE=∠D=60度.所以FC∥BD,又因为∠BAD=∠ABC=60°,所以AD∥BC,即FD∥BC,则四边形BCFD是平行四边形.(2)在Rt△ABC中,设BC=a,则AB=2BC=2a,AD=AB=2a.设AH=x,则HC=HD=AD﹣AH=2a﹣x.在Rt△ABC中,由勾股定理得AC2=3a2 . 在Rt△ACH中,由勾股定理得AH2+AC2=HC2 , 即x2+3a2=(2a﹣x)2 . 解得x= ![]() a,即AH=
a,即AH= ![]() a.求得HC的值后,利用sin∠ACH=AH:HC求值.
a.求得HC的值后,利用sin∠ACH=AH:HC求值.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°,以及对平行四边形的判定的理解,了解两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.


 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,记m=|a﹣b+c|+|2a+b+c|,n=|a+b+c|+|2a﹣b﹣c|.则下列选项正确的是( ) 
A.m<n
B.m>n
C.m=n
D.m、n的大小关系不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市一中准备组织学生及学生家长到武汉大学参观体验,为了便于管理,所有人员到武汉必须乘坐在同一列动车上;根据报名人数,若都买 一等座单程火车票需2556元,若都买二等座单程火车票且花钱最少,则需1530元;已知学生家长与教师的人数之比为2:1,安陆到武汉的动车票价格(动 车学生票只有二等座可以打6折)如下表所示:
(1)参加参观体验的老师、家长与学生各有多少人?
(2)由于各种原因,二等座火车票单程只能买x张(x小于参加参观体验的人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y与x之间的函数关系式.
(3)请你做一个预算,按第(2)小题中的购票方案,购买单程火车票的总费用至少是多少钱?最多是多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与y轴相交于点A(0,3),与x正半轴相交于点B,对称轴是直线x=1
(1)求此抛物线的解析式以及点B的坐标.
(2)动点M从点O出发,以每秒2个单位长度的速度沿x轴正方向运动,同时动点N从点O出发,以每秒3个单位长度的速度沿y轴正方向运动,当N点到达A点时,M、N同时停止运动.过动点M作x轴的垂线交线段AB于点Q,交抛物线于点P,设运动的时间为t秒.
①当t为何值时,四边形OMPN为矩形.
②当t>0时,△BOQ能否为等腰三角形?若能,求出t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果任意选择一对有序整数(m,n),其中|m|≤1,|n|≤3,每一对这样的有序整数被选择的可能性是相等的,那么关于x的方程x2+nx+m=0有两个相等实数根的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com