
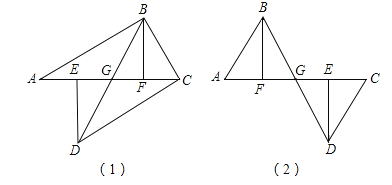
【题目】如图(1),A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC,若AB=CD,试证明BD平分EF,若将△DEC的边EC沿AC方向移动变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.
【答案】(1)证明见试题解析;(2)成立.
【解析】
试题分析:(1)先利用HL判定Rt△ABF≌Rt△CDE,得出BF=DE;再利用AAS判定△BFG≌△DEG,从而得出FG=EG,即BD平分EF;
(2)结论仍然成立,同样可以证明得到.
试题解析:(1)证明:∵DE⊥AC,BF⊥AC,∴∠DEG=∠BFE=90°,∵AE=CF,AE+EF=CF+EF,即AF=CE.在Rt△ABF和Rt△CDE中,∵AB=CD,AF=CE,∴Rt△ABF≌Rt△CDE(HL),∴BF=DE.在△BFG和△DEG中,∵∠BFG=∠DEG,∠BGF=∠DGE,BF=DE,∴△BFG≌△DEG(AAS),∴FG=EG,即BD平分EF;
(2)FG=EG,即BD平分EF的结论依然成立.
理由:如图2,连接BE、FD.∵AE=CF,FE=EF,∴AF=CE,∵DE垂直于AC,BF垂直于AC,∴∠AFB=∠CED,BF∥DE,∴在Rt△ABF和Rt△CDE中,∵AF=CE,AB=CD,∴△ABF≌△CDE(HL),∴BF=DE,∴四边形BEDF是平行四边形,∴GE=GF,即:BD平分EF,即结论依然成立.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系,请你从所得到的关系中任选一个加以说明。(适当添加辅助线,其实并不难)




(1) (2) (3) (4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市2012年底已有绿化面积300公顷,经过两年绿化,绿化面积逐年增加,到2014年底增加到363公顷,设绿化面积平均每年的增长率为x,由题意,所列方程正确的是( )
A.300(1+x)=363
B.300(1+x)2=363
C.300(1+2x)=363
D.363(1﹣x)2=300
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家电信公司推出两种移动电话计费方法:计费方法A是每月收月租费58元,通话时间不超过![]() 分钟的部分免费,超过
分钟的部分免费,超过![]() 分钟的按每分钟0.25元加收通话费;计费方法B是每月收取月租费88元,通话时间不超过
分钟的按每分钟0.25元加收通话费;计费方法B是每月收取月租费88元,通话时间不超过![]() 分钟的部分免费,超过
分钟的部分免费,超过![]() 分钟的按每分钟0.20元收通话费.现在设通话时间是
分钟的按每分钟0.20元收通话费.现在设通话时间是![]() 分钟.
分钟.
(1)当通话时间超过![]() 分钟时,请用含
分钟时,请用含![]() 的代数式表示计费方法A的通话费用.
的代数式表示计费方法A的通话费用.
(2)当通话时间超过![]() 分钟时,请用含
分钟时,请用含![]() 的代数式表示计费方法B的通话费用.
的代数式表示计费方法B的通话费用.
(3)用计费方法A的用户一个月累计通话360分钟所需的话费,若改用计费方法B,则可通话多少分钟?
(4)请你分析,当通话时间超过多少分钟时采用计费方法B合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
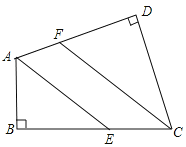
【题目】已知:如图,四边形ABCD中,AD⊥DC,BC⊥AB,AE平分∠BAD,CF平分∠DCB,AE交CD于E,CF交AB于F,问AE与CF是否平行?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC中,BF、CF是角平分线,DE∥BC,分别交AB、AC于点D、E,DE经过点F.结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE; ③△ADE的周长=AB+AC;④BF=CF.其中正确的是______.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
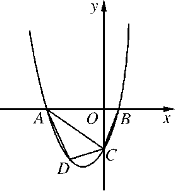
【题目】已知,如图,抛物线![]() >0)与
>0)与![]() 轴交于点C,与
轴交于点C,与![]() 轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在![]() 轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①“掷一枚质地均匀的骰子两次,两次向上的点数都是6”是随机事件;②小概率事件一定不会发生.( )
A.只有①正确B.只有②正确C.①②都正确D.①②都错误
查看答案和解析>>
科目:初中数学 来源: 题型:
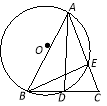
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.
求证:(1)、D是BC的中点;(2)、△BEC∽△ADC;(3)、若![]() ,求⊙O的半径。
,求⊙O的半径。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com