
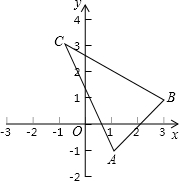
 如图,△ABC在平面直角坐标系中,点A(1,-1),点B(3,1),点C(-1,3),将△ABC绕点O旋转90°后得△A1,B1,C1,求点A1,B1,C1的坐标.
如图,△ABC在平面直角坐标系中,点A(1,-1),点B(3,1),点C(-1,3),将△ABC绕点O旋转90°后得△A1,B1,C1,求点A1,B1,C1的坐标. 分析 利用旋转的性质,分别画出△ABC绕点O顺时针或逆时针旋转90°后得△A1B1C1,然后利用所画图形分别写出对应的点A1,B1,C1的坐标.
解答 解:当△ABC绕点O顺时针旋转90°后得△A1B1C1,如图1,点A1,B1,C1的坐标分别为(-1,-1),(1,-3),(3,1);
当△ABC绕点O逆时针旋转90°后得△A1B1C1,如图2,点A1,B1,C1的坐标分别为(1,1),(-1,3),(-3,-1).

点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75,其图象如图所示.
某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75,其图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
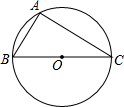 如图,已知BC为⊙O的直径,△ABC内接于⊙O,AB=2,∠C=30°.
如图,已知BC为⊙O的直径,△ABC内接于⊙O,AB=2,∠C=30°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
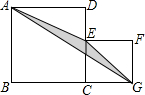 如图,正方形ABCD和EFGC中,左右两个正方形边长分别为a、b,用代数式表示阴影部分△AEG的面积为( )
如图,正方形ABCD和EFGC中,左右两个正方形边长分别为a、b,用代数式表示阴影部分△AEG的面积为( )| A. | a2-b2 | B. | $\frac{2}{3}({a}^{2}-{b}^{2})$ | C. | $\frac{1}{2}{b}^{2}$ | D. | $\frac{1}{2}{a}^{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com