
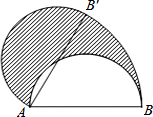
 如图,直径AB为4的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是$\frac{8π}{3}$.
如图,直径AB为4的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是$\frac{8π}{3}$. 分析 根据题意得出AB=AB′=4,∠BAB′=60°,根据图形得出图中阴影部分的面积S=$\frac{60π×{4}^{2}}{360}$+$\frac{1}{2}$π×42-$\frac{1}{2}$π×42即可得到结论.
解答 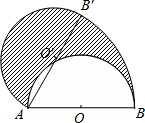 解:∵AB=AB′=4,∠BAB′=60°
解:∵AB=AB′=4,∠BAB′=60°
∴图中阴影部分的面积是:
S=S扇形B′AB+S半圆O′-S半圆O
=$\frac{60π×{4}^{2}}{360}$+$\frac{1}{2}$π×22-$\frac{1}{2}$π×42
=$\frac{8π}{3}$π.
故答案为:$\frac{8π}{3}$.
点评 本题主要考查了扇形的面积的计算,正确理解阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积-以AB为直径的半圆的面积=扇形ABB′的面积是解题的关键.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
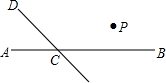 如图,直线CD与直线AB相交于C,根据下列语句画图
如图,直线CD与直线AB相交于C,根据下列语句画图查看答案和解析>>
科目:初中数学 来源: 题型:选择题
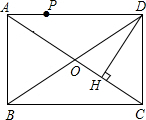 如图,点P是矩形ABCD所得边AD上的一个动点.DH⊥AC于H,那么点P到矩形的两条对角线AC和BD的距离之和等于( )
如图,点P是矩形ABCD所得边AD上的一个动点.DH⊥AC于H,那么点P到矩形的两条对角线AC和BD的距离之和等于( )| A. | 2DH | B. | $\frac{3}{2}DH$ | C. | DH | D. | $\frac{2}{3}DH$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,将长方形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(5,4),则点E的坐标为(5,$\frac{3}{2}$).
如图,在平面直角坐标系中,将长方形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(5,4),则点E的坐标为(5,$\frac{3}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
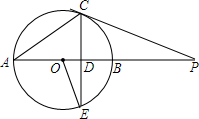 如图,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点D,连结OE、AC,已知∠POE=2∠CAB.
如图,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点D,连结OE、AC,已知∠POE=2∠CAB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com