
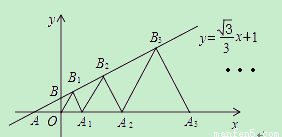
在平面直角坐标系中,直线l:y= x+1交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的周长是( )
x+1交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的周长是( )
A.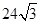 B.
B.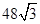
C.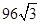 D.
D.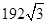
C
【解析】首先求得点A与B的坐标,即可求得∠OAB的度???,又由△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形,易求得OB1=OA=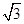 ,A1B1=A1A,A2B2=A2A,则可得规律:OAn=(2n﹣1)
,A1B1=A1A,A2B2=A2A,则可得规律:OAn=(2n﹣1)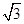 .根据A5A6=OA6﹣OA5求得△A5B6A6的边长,进而求得周长.
.根据A5A6=OA6﹣OA5求得△A5B6A6的边长,进而求得周长.
【解析】
∵直线l的解析式为y=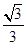 x+1且交x轴于点A,交y轴于点B,
x+1且交x轴于点A,交y轴于点B,
∴点A(﹣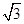 ,0),点B(0,1),
,0),点B(0,1),
∴OA=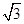 ,OB=1,
,OB=1,
∴tan∠OAB=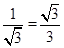 ,
,
∴∠OAB=30°,
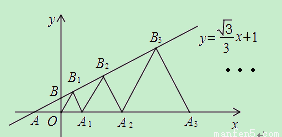
∵△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形,
∴∠A1OB1=∠A2A1B2=∠A3A2B3=60°,
∴∠OB1A=∠A1B2A=∠A2B3A=∠OAB=30°,
∴OB1=OA=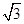 ,A1B2=A1A,A2B3=A2A,
,A1B2=A1A,A2B3=A2A,
∴OA1=OB1=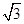 ,OA2=OA1+A1A2=OA1+A1B2=
,OA2=OA1+A1A2=OA1+A1B2=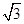 +2
+2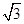 =3
=3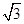 ,
,
同理:OA3=7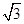 ,OA4=15
,OA4=15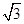 ,OA5=31
,OA5=31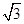 ,OA6=63
,OA6=63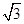 ,
,
则A5A6=OA6﹣OA5=32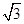 .
.
则△A5B6A6的周长是96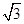 ,
,
故选C.


科目:初中数学 来源:2014中考名师推荐数学概率(解析版) 题型:选择题
如图所示为一个污水净化塔内部,污水从上方入口进入后流经形如等腰直角三角形的净化材枓表面,流向如图中箭头所示,每一次水流流经三角形两腰的机会相同,经过四层净化后流入底部的5个出口中的一个.下列判断:①5个出口的出水量相同;②2号出口的出水量与4号出口的出水量相同;③1,2,3号出水口的出水量之比约为1:4:6;④若净化材枓损耗的速度与流经其表面水的数量成正比,则更换最慢的一个三角形材枓使用的时间约为更换最快的一个三角形材枓使用时间的8倍.其中正确的判断有( )个.

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:解答题
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连接CD、QC.
(1)求当t为何值时,点Q与点D重合?
(2)设△QCD的面积为S,试求S与t之间的函数关系式,并求S的最大值;
(3)若⊙P与线段QC只有一个交点,请直接写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:选择题
如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O切线,切点为B,连结AC交⊙O于D,∠C=38°.点E在AB右侧的半圆上运动(不与A、B重合),则∠AED的大小是( )

A.19°
B.38°
C.52°
D.76°
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的相似(解析版) 题型:填空题
如图,正方形ABCD的边长为4,E、F分别是BC、CD上的两个动点,且AE⊥EF.则AF的最小值是____________.

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的折叠(解析版) 题型:填空题
如图,在△ABC中,AB=AC,BC=8,tanC=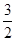 ,如果将△ABC沿直线l翻折后,点B落在边AC的中点处,直线l与边BC交于点D,那么BD的长为 .
,如果将△ABC沿直线l翻折后,点B落在边AC的中点处,直线l与边BC交于点D,那么BD的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com