
【题目】如图,AD, CE为ΔABC的角平分线且交于0点,∠DAC=30°,∠ECA=35°,则∠AOB=_______。

【答案】125°
【解析】
根据角平分线的定义可得出∠BAC=60°、∠ACB=70°,结合三角形内角和可得出∠ABC=50°,由三角形的三条角平分线交于一点,可得出BO平分∠ABC,进而可得出∠ABO的度数,进而可求出∠AOB的度数.
解:∵AD平分∠BAC,CE平分∠ACB,∠DAC=30°,∠ECA=35°,
∴BAD=∠DAC=30°,,∠BAC=2∠DAC=60°,∠ACB=2∠ECA=70°,
∴∠ABC=180°-∠BAC-∠ACB=50°.
∵△ABC的三条角平分线交于一点,
∴BO平分∠ABC,
∴∠ABO=![]() ∠ABC=25°,
∠ABC=25°,
∴∠AOB=180°-30°-25°=125°.
故答案为:125°.


科目:初中数学 来源: 题型:
【题目】某校初二年级数学考试,(满分为100分,该班学生成绩均不低于50分)作了统计分析,绘制成如图频数分布直方图和频数、频率分布表,请你根据图表提供的信息,解答下列问题:
分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
频数 | 2 | a | 20 | 16 | 4 | 50 |
频率 | 0.04 | 0.16 | 0.40 | 0.32 | b | 1 |

(1)频数、频率分布表中a= ,b= ;(答案直接填在题中横线上)
(2)补全频数分布直方图;
(3)若该校八年级共有600名学生,且各个班级学生成绩分布基本相同,请估计该校八年级上学期期末考试成绩低于70分的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】ΔABC、ΔCDE都是等边三角形,AD、BE相交于点O,点M、点N分别是线段AD、BE的中点.
(1)证明: AD=BE.(2)求∠DOE的角度。(3)证明:ΔMNC是等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A:篮球 B:乒乓球C:羽毛球 D:足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:


(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC、△DCE均为等边三角形,当B、C、E三点在同一条直线上时,连接BD、AE交于点F,易证:△ACE≌△BCD.聪明的小明将△DCE绕点C旋转的过程中发现了一些不变的结论,让我们一起开启小明的探索之旅!

(探究一)如图2,当B、C、E三点不在同一条直线上时,小明发现∠BFE的大小没有发生变化,请你帮他求出∠BFE的度数.

(探究二)阅读材料:在平时的练习中,我们曾探究得到这样一个正确的结论:两个全等三角形的对应边上的高相等.例如:如图3,如果△ABC≌△A’B’C’,AD、A’D’分别是△ABC、△A’B’C’的边BC、B’C’上的高,那么容易证明AD=A’D’.小明带着这样的思考又有了新的发现:如图4,若连接CF,则CF平分∠BFE,请你帮他说明理由.

(探究三)在探究二的基础上,小明又进一步研究发现,线段AF、BF、CF之间还存在一定的数量关系,请你写出它们之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华有一个容量为8GB (1GB= 1024MB)的U盘,U盘中已经存储了一个视频文件,其余空间都用来存储照片,若每张照片占用的内存容量均相同,图片数量x (张)和剩余可用空间y (MB)的部分关系如表:
图片数量 | 100 | 150 | 200 | 400 | 800 |
剩余可用空间 | 5700 | 5550 | 5400 | 4800 | 3600 |
(1)由上表可知,y与x之间满足___ ___(填“一次”或“二次”或“反比例”)函数的关系,求出y与x之间的关系式.
(2)求出U盘中视频文件的占用内存容量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:
①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=![]() MF.其中正确结论的是( )
MF.其中正确结论的是( )

A. ①③④ B. ②④⑤ C. ①③④⑤ D. ①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
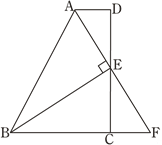
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F. 已知AD=2cm,BC=5cm.
(1)求证:FC=AD;
(2)求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于![]() BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D,连接CD,若CD=AD,∠B=20°,则下列结论中错误的是( )
BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D,连接CD,若CD=AD,∠B=20°,则下列结论中错误的是( )

A. ∠CAD=40° B. ∠ACD=70° C. 点D为△ABC的外心 D. ∠ACB=90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com