
����Ŀ����ͼ����֪���κ���L1��y=ax2-2ax+a+3��a��0���Ͷ��κ���L2��y=-a��x+1��2+1��a��0��ͼ��Ķ���ֱ�ΪM��N����y��ֱ��ڵ�E��F��
��1������y=ax2-2ax+a+3��a��0������СֵΪ�� �� �����κ���L1 �� L2��yֵͬʱ����x���������Сʱ��x��ȡֵ��Χ��
��2����EF=MNʱ����a��ֵ�����ж��ı���ENFM����״��ֱ��д��������֤������
��3�������κ���L2��ͼ����x����ҽ���ΪA��m��0��������AMNΪ����������ʱ����-a��x+1��2+1=0�Ľ⣮
���𰸡�
��1��3����1��x��1
��2��
�⣺�ɶ��κ���L1��y=ax2-2ax+a+3��֪E��0��a+3����
�ɶ��κ���L2��y=-a��x+1��2+1=��a2x-2ax-a+1��֪F��0��-a+1����
��M��1��3����N��-1��1����
��EF=MN=![]() =2
=2![]() ��
��
��a+3-��-a+1��=2![]() ��
��
��a=![]() -1��
-1��
��MG��y����G����MG=1����NH��y����H����NH=1��
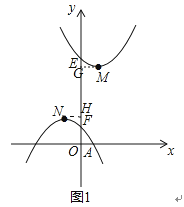
��MG=NH=1��
��EG=a+3-3=a��FH=1-��-a+1��=a��
��EG=FH��
�ڡ�EMG�͡�FNH�У�
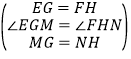 ��
��
���EMG�ա�FNH��SAS����
���MEF=��NFE��EM=NF��
��EM��NF��
���ı���ENFM��ƽ���ı��Σ�
��EF=MN��
���ı���ENFM�Ǿ���
��3��
�⣺�ɡ�AMNΪ���������Σ��ɷ�Ϊ�������������
����ͼ2��
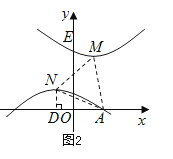
��MN=NA=2![]() ʱ������N��ND��x�ܣ�����Ϊ��D������ND=1��DA=m-��-1��=m+1��
ʱ������N��ND��x�ܣ�����Ϊ��D������ND=1��DA=m-��-1��=m+1��
��Rt��NDA��NA2=DA2+ND2������2![]() ��2=��m+1��2+12��
��2=��m+1��2+12��
��m1=![]() -1��m2=-
-1��m2=-![]() -1���������⣬��ȥ����
-1���������⣬��ȥ����
��A��![]() -1��0����
-1��0����
��������y=-a��x+1��2+1��a��0���ĶԳ���Ϊx=-1��
������x�����һ����������Ϊ��-1-![]() ��0����
��0����
���-a��x+1��2+1=0�Ľ�Ϊx1=![]() ��1��x2=-1-
��1��x2=-1-![]() ��
��
����ͼ3��
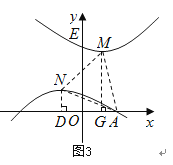
��MA=NAʱ������M��MG��x�ᣬ����ΪG������OG=1��MG=3��GA=|m-1|��
����Rt��MGA��MA2=MG2+GA2����MA2=32+��m-1��2��
�֡�NA2=��m+1��2+12��
�ࣨm+1��2+12=32+��m-1��2��m=2��
��A��2��0����
��������y=-a��x+1��2+1��a��0������������-4��0����
���-a��x+1��2+1=0�Ľ�Ϊx1=2��x2=-4��
�۵�MN=MAʱ��32+��m-1��2=��2![]() ��2��
��2��
��m��ʵ���⣬��ȥ��
��������������AMNΪ����������ʱ������-a��x+1��2=0�Ľ�Ϊ
x1=![]() -1��x2=-1-
-1��x2=-1-��x1=2��x2=-4��
����������1���Ѷ��κ���L1��y=ax2-2ax+a+3���ɶ���ʽ�����������Сֵ���ֱ���ö��κ���L1 �� L2��yֵ����x���������С��x��ȡֵ���Ӷ���ö��κ���L1 �� L2��yֵͬʱ����x���������Сʱ��x��ȡֵ��Χ��
��2�������E��F������꣬��MG��y����G����MG=1����NH��y����H����NH=1���Ӷ����MG=NH=1��Ȼ��֤�á�EMG�ա�FNH����MEF=��NFE��EM=NF������֤��EM��NF���Ӷ��ó��ı���ENFM��ƽ���ı��Σ�
��3����MN�Ĵ�ֱƽ���ߣ���MN��D����x����A�������D�����꣬�̶����MN�Ľ���ʽ�������Ϳ����ֱ��AD�Ľ���ʽ����y=0�����A�����꣬���ݶԳ���Ӷ������һ����������꣬�Ϳ���÷���-a��x+1��2+1=0�Ľ⣮
���⿼���˶��κ������ۺ�Ӧ�ã�������������ʽ�����������⣬ƽ���ı����ж������������ε�.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߳�Ϊ6cm��������ABCD�۵���ʹ��D����AB�ߵ��е�E�����ۺ�ΪFH����C����Q����EQ��BC���ڵ�G�����EBG���ܳ���cm�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��AOB�У���AOB=90�㣬AO=![]() ��BO=1��AB�Ĵ�ֱƽ���߽�AB�ڵ�E��������BO�ڵ�F����P�ӵ�A����������AO��ÿ��
��BO=1��AB�Ĵ�ֱƽ���߽�AB�ڵ�E��������BO�ڵ�F����P�ӵ�A����������AO��ÿ��![]() ����λ���ٶ��˶���ͬʱ��Q�ӵ�O������OB������ÿ��1����λ���ٶ��˶�������Q�����Bʱ����P��Qͬʱֹͣ�˶������˶���ʱ��Ϊt�룮
����λ���ٶ��˶���ͬʱ��Q�ӵ�O������OB������ÿ��1����λ���ٶ��˶�������Q�����Bʱ����P��Qͬʱֹͣ�˶������˶���ʱ��Ϊt�룮
��1����t= ʱ��PQ��EF��
��2����P��Q���ڵ�O�ĶԳƵ�ֱ�ΪP�䡢Q�䣬���߶�P��Q�����߶�EF�й�����ʱ��t��ȡֵ��Χ�� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx��a��0��������A��2��0������B��3��3����BC��x���ڵ�C������OB������ֱ��������DEF��б��EF��x���ϣ���E������Ϊ����4��0������F��ԭ���غ�
��1���������ߵĽ���ʽ��ֱ��д�����ĶԳ��
��2����DEF��ÿ��1����λ���ȵ��ٶ���x���������ƶ����˶�ʱ��Ϊt�룬����D����BC����ʱֹͣ�˶������DEF���OBC���ص����ֵ����ΪS�����S����t�ĺ�����ϵʽ��
��3����P�������߶Գ�����һ�㣬����ABP��ֱ��������ʱ����ֱ��д�����з��������ĵ�P���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ĵ�����װ�н���ɫ��ͬ��10��С�����к���4��������6����
��1���ȴӴ�����ȡ��m��m��1���������ٴӴ������������1��������������Ϊ�¼�A����������б���
�¼�A | ��Ȼ�¼� | ����¼� |
m��ֵ |
��2���ȴӴ�����ȡ��m�������ٷ���m��һ���ĺ���ҡ�ȣ��������1������ĸ��ʵ���![]() ����m��ֵ��
����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��дһ����ϲ����ʵ��m��ֵ ��ʹ���¼������ڶ��κ���![]() ����x����3ʱ��y��x���������С����Ϊ����¼���
����x����3ʱ��y��x���������С����Ϊ����¼���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ�������dz����ĵ�ש�ϵ�ͼ�������а�����һ�������ƽ��ͼ�Ω����˱��Σ�
��1����ͼ�ڣ�AE�ǡ�O��ֱ������ֱ�ߺ�Բ������O���ڽ����˱���ABCDEFGH����д������������ͼ�ۼ�����
��2���ڣ�1����ǰ���£�����OD����֪OA=5��������OAD����AOD��180�㣩��һ��Բ�IJ��棬�����Բ����Բ�İ뾶����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ABC�����Ϊ1����ͼ�٣�����BC��AC�ֱ�2�ȷ֣�BE1��AD1�ཻ�ڵ�O����AOB�������ΪS1����ͼ�ڽ���BC��AC�ֱ�3�ȷ֣�BE1��AD1�ཻ�ڵ�O����AOB�������ΪS2�������������ƣ���Sn�ɱ�ʾΪ�� �����ú�n�Ĵ���ʽ��ʾ������nΪ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y=![]() x��ͼ����ͼ��ʾ��������κ���y=ax2��4ax+c��ͼ����A��B���㣨���е�A�ڵ�B����ࣩ����������κ���ͼ��ĶԳ��ύ�ڵ�C��
x��ͼ����ͼ��ʾ��������κ���y=ax2��4ax+c��ͼ����A��B���㣨���е�A�ڵ�B����ࣩ����������κ���ͼ��ĶԳ��ύ�ڵ�C��
��1�����C������
��2������κ���ͼ��Ķ���ΪD��
������D���C����x��Գƣ��ҡ�ACD���������3����˶��κ����Ĺ�ϵʽ��
����CD=AC���ҡ�ACD���������10����˶��κ����Ĺ�ϵʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com