
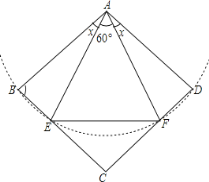
【题目】已知四边形![]() 是菱形,
是菱形,![]() 是正三角形,
是正三角形,![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() ,则
,则![]() ____度.
____度.
【答案】![]()
【解析】
设∠BAE=x,根据正方形的性质、等边三角形的性质及已知条件,易证△ABE≌△ADF;根据全等三角形的性质可得∠BAE=∠DAF=x,再求得∠BAE的度数,即可求得∠BAD的度数.
设∠BAE=x,
∵四边形ABCD是菱形,△AEF是正三角形,EF=CD,
∵AE=AF=EF=CD=AB=AD,∠B=∠D,
∴∠B=∠D=∠AEB=∠AFD,
∴△ABE≌△ADF,
∴∠BAE=∠DAF=x,
∵BC∥AD,
∴∠AEB=∠EAD,
∴∠ABC=∠AEB=∠EAF+∠DAF=60°+x,
∵∠ABC+∠AEB+∠BAE=180°,
∴60°+x+60°+x+x=180°,
∴x=20°,
∴∠BAE=20°
∴∠BAD=20°+60°+20°=100°.
故答案为100.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过点
的图象经过点![]() ,对称轴是经过
,对称轴是经过![]() 且平行于
且平行于![]() 轴的直线.
轴的直线.

![]() 求
求![]() 、
、![]() 的值;
的值;
![]() 如图,一次函数
如图,一次函数![]() 的图象经过点
的图象经过点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,与二次函数的图象相交于另一点
,与二次函数的图象相交于另一点![]() ,点
,点![]() 在点
在点![]() 的右侧,
的右侧,![]() ,求一次函数的表达式.
,求一次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三年级(1)班要举行一场毕业联欢会.规定每个同学分别转动下图中两个可以自由转动的均匀转盘A、B(转盘A被均匀分成三等份.每份分別标上1.2,3三个钕宇.转盘B被均匀分成二等份.每份分别标上4,5两个数字).若两个转盘停止后指针所指区域的数字都为偶数(如果指针恰好指在分格线上.那么重转直到指针指向某一数字所在区域为止).则这个同学要表演唱歌节目.请求出这个同学表演唱歌节目的概率(要求用画树状图或列表方法求解)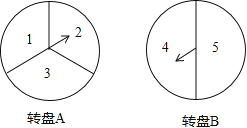
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
若一个整数能表示成a2+b2(a、b是整数)的形式,则称这个数为“平和数”,例如5是“平和数”,因为5=22+1,再如,M=x2+2xy+2y2=(x+y)2+y2(x, y是整数),我们称M也是“平和数”.
(1)请你写一个小于5的“平和数”,并判断34是否为“平和数”.
(2)已知S=x2+9y2+6x﹣6y+k(x,y是整数,k是常数,要使S为“平和数”,试求出符合条件的一个k值,并说明理由.
(3)如果数m,n都是“平和数”,试说明![]() 也是“平和数”.
也是“平和数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰梯形![]() 中,
中,![]() ,对角线
,对角线![]() 于
于![]() 点,点
点,点![]() 在
在![]() 轴上,点
轴上,点![]() 、
、![]() 在
在![]() 轴上.
轴上.
![]() 若
若![]() ,
,![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 若
若![]() ,
,![]() ,求过
,求过![]() 点的反比例函数的解析式;
点的反比例函数的解析式;
![]() 如图,在
如图,在![]() 上有一点
上有一点![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,在
,在![]() 上取
上取![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,当
,当![]() 在
在![]() 上运动时,(不与
上运动时,(不与![]() 、
、![]() 重合),
重合),![]() 的值是否发生变化?若变化,求出变化范围;若不变,求出其值.
的值是否发生变化?若变化,求出变化范围;若不变,求出其值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形![]() 中,
中,![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 的中点,
的中点,![]() 分别交
分别交![]() 、
、![]() 于
于![]() 、
、![]() .请判断下列结论:
.请判断下列结论:![]() ;
;![]() ;
;![]() ;
;![]() .其中正确的结论有( )
.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】选取二次三项式![]() 中的两项,配成完全平方式的过程叫做配方.例如
中的两项,配成完全平方式的过程叫做配方.例如
①选取二次项和一次项配方:![]() ;
;
②选取二次项和常数项配方:![]() ,或
,或![]() ;
;
③选取一次项和常数项配方:![]() .
.
根据上述材料,解决下面问题:
![]() 写出
写出![]() 的两种不同形式的配方;
的两种不同形式的配方;
![]() 若
若![]() ,求
,求![]() 的值;
的值;
![]() 若关于
若关于![]() 的代数式
的代数式![]() 是完全平方式,求
是完全平方式,求![]() 的值;
的值;
![]() 用配方法证明:无论
用配方法证明:无论![]() 取什么实数时,总有
取什么实数时,总有![]() 恒成立.
恒成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】悦达汽车4S店“十一”黄金周销售某种型号汽车,该型号汽车的进价为30万元/辆,若黄金周期间销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,黄金周期间销售量不会突破30台.已知该型号汽车的销售价为32万元/辆,悦达汽车4S店计划黄金周期间销售利润25万元,那么需售出多少辆汽车?(注:销售利润=销售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠B=90°,AB=2,BC=1,CD=2,AD=3,连接AC.
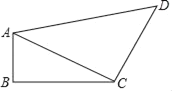
(1)求AC的长;
(2)判断三角形ACD的形状,并求出四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com