
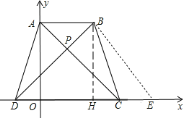
【题目】如图,在等腰梯形![]() 中,
中,![]() ,对角线
,对角线![]() 于
于![]() 点,点
点,点![]() 在
在![]() 轴上,点
轴上,点![]() 、
、![]() 在
在![]() 轴上.
轴上.
![]() 若
若![]() ,
,![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 若
若![]() ,
,![]() ,求过
,求过![]() 点的反比例函数的解析式;
点的反比例函数的解析式;
![]() 如图,在
如图,在![]() 上有一点
上有一点![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,在
,在![]() 上取
上取![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,当
,当![]() 在
在![]() 上运动时,(不与
上运动时,(不与![]() 、
、![]() 重合),
重合),![]() 的值是否发生变化?若变化,求出变化范围;若不变,求出其值.
的值是否发生变化?若变化,求出变化范围;若不变,求出其值.


【答案】(1)![]() ;(2):
;(2):![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据等腰三角形的性质知:AD=BC,在Rt△AOD中,已知AD,OA的长,可将OD的长求出,从而可知点D的坐标;
(2)作辅助线,作BH⊥DE于H,过B点作BE∥AC交x轴于点E,则四边形ABEC为平行四边形,AB=CE,BE=AC,由AC⊥BD,可得:BD⊥BE,故在Rt△BDE中,由斜边DE的长可知:BH的长,在Rt△BHC中,运用勾股定理可将CH的长求出,进而可将OH的长求出,知点B的坐标,从而可求出求过B点的反比例函数的解析式;
(3)作辅助线,过点D作DN∥PC交PE的延长线于点M,交HF的延长线于点N,过点M作MI∥EF交BN于点I,易证四边形EFIM和四边形MNHP是平行四边形,从而可证:△EDM≌△IMN,DM=MN,进而可证:△PDM≌△CPQ,DM=PQ=PH,故:![]() =1,为定值.
=1,为定值.
![]() 在等腰梯形
在等腰梯形![]() 中,
中,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() 作
作![]() 于
于![]() ,过
,过![]() 点作
点作![]() 交
交![]() 轴于点
轴于点![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,
又∵![]() 为等腰梯形,
为等腰梯形,
∴![]() ,
,
∴![]() ,
,
而![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 为
为![]() 的中点,即
的中点,即![]() 为直角三角形
为直角三角形![]() 斜边
斜边![]() 上的中线,
上的中线,
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴过![]() 点的反比例函数的解析式为:
点的反比例函数的解析式为:![]() ;
;
![]() 过点
过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
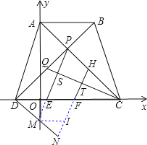
易证四边形![]() 和四边形
和四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
由![]() 知:
知:![]() ,而
,而![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣bx+c交x轴于点A(1,0),交y轴于点B,对称轴是x=2.

(1)求抛物线的解析式;
(2)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△ACE≌△ACF;
(2)若AB=21,AD=9,AC=17,求CF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是________(填A或B或C)
A.a2-2ab+b2=(a-b)2
B.a2-b2=(a+b)(a-b)
C.a2+ab=a(a+b)
(2)应用你从(1)中选出的等式,完成下列各题:
①已知x2-4y2=12,x+2y=4,求x-2y的值
②计算:(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )…(1-
)…(1-![]() )(1-
)(1-![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的反比例函数,并且当
的反比例函数,并且当![]() 时,
时,![]() .
.
![]() 求
求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
![]() 当
当![]() 时,
时,![]() 的值为________;该函数的图象位于第________象限,在图象的每一支上,
的值为________;该函数的图象位于第________象限,在图象的每一支上,![]() 随
随![]() 的增大而________.
的增大而________.
![]() 直接写出此反比例函数与直线
直接写出此反比例函数与直线![]() 的交点坐标.
的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 如果把一个三角形的各边扩大为原来的![]() 倍,那么它的周长也扩大为原来的
倍,那么它的周长也扩大为原来的![]() 倍
倍
B. 相似三角形对应高的比等于对应中线的比
C. 相似多边形的面积比等于周长比的平方
D. 如果把一个多边形的面积扩大为原来的![]() 倍,那么它的各边也扩大为原来的
倍,那么它的各边也扩大为原来的![]() 倍
倍
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,且
点,且![]() .
.

![]() 求抛物线的解析式及顶点
求抛物线的解析式及顶点![]() 的坐标;
的坐标;
![]() 判断
判断![]() 的形状,证明你的结论;
的形状,证明你的结论;
![]() 点
点![]() 是
是![]() 轴上的一个动点,当
轴上的一个动点,当![]() 的周长最小时,求点
的周长最小时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
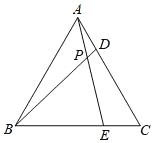
【题目】如图,△ABC 为等边三角形,D、E 分别是边 AC、BC 上的点,且AD=CE,AE 与 BD 相交于点 P.
(1)求∠BPE 的度数;
(2)若 BF⊥AE 于点 F,试判断 BP 与 PF 的数量关系并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com