Question

【题目】已知是的反比例函数，并且当时，．

求关于的函数解析式；

当时，的值为________；该函数的图象位于第________象限，在图象的每一支上，随的增大而________．

直接写出此反比例函数与直线的交点坐标．

Answer 1

【答案】（1）；（2）；一、三；减小．和．

【解析】

（1）根据点（2，8）利用待定系数法即可求出反比例函数解析式；

（2）将x＝4代入反比例函数解析式中求出y值，再由k＝16＞0结合反比例函数图象即可得出结论；

（3）联立两函数解析式成方程组，通过解方程组即可求出两函数图象的交点坐标．

（1）设y关于x的函数解析式为y＝（k≠0），

将（2，8）代入y＝，

8＝，解得：k＝16，

∴y关于x的函数解析式为y＝．

（2）当x＝4时，y＝＝4；

∵k＝16＞0，

∴反比例函数y＝的图象位于第一、三象限，且在图象的每一支上，y随x的增大而减小．

故答案为：4；一、三；减小．

3）联立两函数解析式成方程组，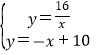

解得：，．

∴此反比例函数与直线y＝x＋10的交点坐标为（2，8）和（8，2）．