Question

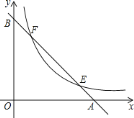
【题目】如图，已知直线分别与轴，轴交于，两点，与双曲线交于，两点，若，则的值是________．

Answer 1

【答案】

【解析】

试题作FH⊥x轴，EC⊥y轴，FH与EC交于D，先利用一次函数图象上点的坐标特征得到A（2，0），B（0， 2），易得△AOB为等腰直角三角形，则AB=OA=2，所以EF=AB=，且△DEF为等腰直角三角形，则FD=DE=EF=1；设F点坐标为（t，-t+2），则E点坐标为（t+1，-t+1），根据反比例函数图象上点的坐标特征得到t（-t+2）=（t+1）（-t+1），解得t=，这样可确定E点坐标为（，），然后根据反比例函数图象上点的坐标特征得到k=×．

试题解析：作FH⊥x轴，EC⊥y轴，FH与EC交于D，如图，

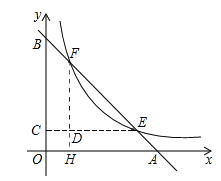
A点坐标为（2，0），B点坐标为（0，2），OA=OB，

∴△AOB为等腰直角三角形，

∴AB=OA=2，

∴EF=AB=，

∴△DEF为等腰直角三角形，

∴FD=DE=EF=1；

设F点横坐标为t，代入y=-x+2，则纵坐标是-t+2，则F的坐标是：（t，-t+2），E点坐标为（t+1，-t+1），

∴t（-t+2）=（t+1）（-t+1），解得t=

∴E点坐标为（，）

∴k=×=．