Question

【题目】已知，如图，垂直，AB=6，Δ是等边三角形，点在射线上运动，以为边向右上方作等边Δ，射线与射线交于点.

（1）如图1，当点运动到与点成一条直线时， （填长度），∠ 度.

（2）在图2中，①求证：∠；

②随着点的运动，∠的度数是否发生改变？若不变，求出这个角的度数；若改变，说明理由.

Answer 1

【答案】（1）12，60；（2）①证明见详解；②∠QFC的度数不变，∠QFC=60°；理由见详解.

【解析】

（1）如图1，根据题意，由等边三角形的性质得到PQ=AP，∠BAP=∠ABE=60°，根据三角形的内角和得到∠APB=∠EBP=30°，根据直角三角形的性质得到AP=2AB=12，BE=PE，证得QF⊥AP，即可得到结论；

（2）①根据等边三角形的性质可以得出AB=AE，AP=AQ，由等式的性质就可以得出∠BAP=∠EAQ，就可以得出结论；

②根据三角形的外角等于不相邻的两内角的和，证明∠BAP=∠EAQ，进而得到△ABP≌△AEQ，证得∠AEQ=∠ABP=90°，则∠BEF=180°-∠AEQ-∠AEB=180°-90°-60°=30°，∠QFC=∠EBF+∠BEF．

解：（1）如图1，当点P运动到与A、E成一直线时，

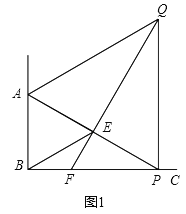
∵△ABE与△APQ是等边三角形，

∴PQ=AP，∠BAP=∠ABE=60°，

∵∠ABP=90°，

∴∠APB=∠EBP=30°，

∴AP=2AB=12，BE=PE，

∴PQ=AP=12；

∵PE=AE，

∴QF⊥AP，

∴∠QFC=60°，

故答案为：12，60；

（2）①如图2，

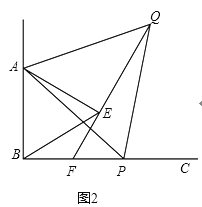
∵△ABE和△APQ是等边三角形，

∴AB=AE，AP=AQ，∠BAE=∠PAQ=∠ABE=∠AEB=60°，

∴∠BAE-∠PAE=∠PAQ-∠PAE，

∴∠BAP=∠EAQ，

在△ABP和△AEQ中，

，

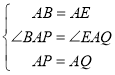∴△ABP≌△AEQ（SAS），

∴∠AEQ=∠ABC=90°．

②∠QFC的度数不变，∠QFC=60°；

由（2）①得∴△ABP≌△AEQ（SAS）

∴∠AEQ=∠ABP=90°

∴∠BEF=180°-∠AEQ-∠AEB=180°-90°-60°=30°，

∴∠QFC=∠EBF+∠BEF=30°+30°=60°．