Question

【题目】已知：如图①，在△ABC中，BC=AC，在△CDE中，CE=CD，现把两个三角形的C点重合，且使∠BCA=∠ECD，连接BE、AD.

(1)求证：BE=AD

(2)若将△ECD绕点C旋转至图②、③所示的情况时，其余条件不变，BE与AD还相等么？若相等，请给与证明；若不相等，请说明理由.

Answer 1

【答案】（1）见解析；（2）BE与AD相等，理由见解析.

【解析】

（1）由∠BCA=∠ECD可推出∠BCE=∠ACD，然后利用SAS即可证明△BCE≌△ACD，从而得到BE=AD；

（2）图②可直接利用SAS即可证明△BCE≌△ACD，从而得到BE=AD；图③先由∠BCA=∠ECD推出∠BCE=∠ACD，然后利用SAS即可证明△BCE≌△ACD，从而得到BE=AD.

证明：（1）∵∠BCA=∠ECD

∴∠BCA－∠ECA=∠ECD－∠ECA

即∠BCE=∠ACD

在△BCE和△ACD中，

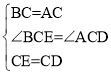
∴△BCE≌△ACD（SAS）

∴BE=AD

（2）BE与AD相等，理由如下：

如图②，在△BCE和△ACD中，

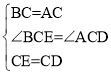
∴△BCE≌△ACD（SAS）

∴BE=AD

如图③，∵∠BCA=∠ECD

∴∠BCA+∠ACE=∠ECD+∠ACE

即∠BCE=∠ACD，

在△BCE和△ACD中，

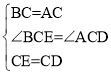
∴△BCE≌△ACD（SAS）

∴BE=AD