
【题目】如图,在某场足球比赛中,球员甲从球门底部中心点![]() 的正前方
的正前方![]() 处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为
处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为![]() 时达到最高点,此时足球飞行的水平距离为
时达到最高点,此时足球飞行的水平距离为![]() .已知球门的横梁高
.已知球门的横梁高![]() 为
为![]() .
.

![]() 在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
![]() 守门员乙站在距离球门
守门员乙站在距离球门![]() 处,他跳起时手的最大摸高为
处,他跳起时手的最大摸高为![]() ,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
【答案】(1)能射中球门;(2)他至少后退![]() ,才能阻止球员甲的射门.
,才能阻止球员甲的射门.
【解析】
(1)、根据条件可以得到抛物线的顶点坐标是(4,3),利用待定系数法即可求得函数的解析式;(2)、求出当x=2时,抛物线的函数值,与2.52米进行比较即可判断,再利用y=2.52求出x的值即可得出答案.
(1)、抛物线的顶点坐标是(4,3), 设抛物线的解析式是:y=a(x-4)2+3,
把(10,0)代入得36a+3=0,解得a=-![]() , 则抛物线是y=-
, 则抛物线是y=-![]() (x-4)2+3,
(x-4)2+3,
当x=0时,y=-![]() ×16+3=3-
×16+3=3-![]() =
=![]() <2.44米, 故能射中球门;
<2.44米, 故能射中球门;
(2)当x=2时,y=-![]() (2-4)2+3=
(2-4)2+3=![]() >2.52, ∴守门员乙不能阻止球员甲的此次射门,
>2.52, ∴守门员乙不能阻止球员甲的此次射门,
当y=2.52时,y=-![]() (x-4)2+3=2.52, 解得:x1=1.6,x2=6.4(舍去), ∴2-1.6=0.4(m),
(x-4)2+3=2.52, 解得:x1=1.6,x2=6.4(舍去), ∴2-1.6=0.4(m),
答:他至少后退0.4m,才能阻止球员甲的射门.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.
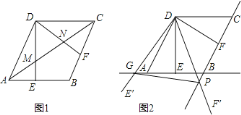
![]() 如图
如图![]() ,连接
,连接![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,求证:
,求证:![]() ;
;
![]() 如图
如图![]() ,将
,将![]() 以点
以点![]() 为旋转中心旋转,其两边
为旋转中心旋转,其两边![]() 、
、![]() 分别与直线
分别与直线![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() ,连接
,连接![]() ,当
,当![]() 的面积等于
的面积等于![]() 时,求旋转角的大小并指明旋转方向.
时,求旋转角的大小并指明旋转方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,CE和BD交于点O,AO的延长线交BC于点F,则图中全等的三角形有( )

A.8对B.7对C.6对D.5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在△ABC中,BC=AC,在△CDE中,CE=CD,现把两个三角形的C点重合,且使∠BCA=∠ECD,连接BE、AD.
(1)求证:BE=AD
(2)若将△ECD绕点C旋转至图②、③所示的情况时,其余条件不变,BE与AD还相等么?若相等,请给与证明;若不相等,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴的一个交点
轴的一个交点![]() 在点
在点![]() 和
和![]() 之间,其部分图象如图所示,则以下结论:①
之间,其部分图象如图所示,则以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④方程以
;④方程以![]() 有两个的实根,其中正确的个数为( )
有两个的实根,其中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级![]() 班有
班有![]() 名同学,其中男生
名同学,其中男生![]() 人.在一节数学课上,老师叫班上每个同学把自己的名字(没有同名)各写在一张大小、形状都相同的小卡片上,并放入一个盒子里摇匀.
人.在一节数学课上,老师叫班上每个同学把自己的名字(没有同名)各写在一张大小、形状都相同的小卡片上,并放入一个盒子里摇匀.
![]() 如果老师随便从盒子中取出一张小卡片,则每个同学被抽到的概率是多少?
如果老师随便从盒子中取出一张小卡片,则每个同学被抽到的概率是多少?
![]() 如果老师随便从盒子中抽出一张小卡片,那么抽到男同学的概率大还是抽到女同学的概率大?
如果老师随便从盒子中抽出一张小卡片,那么抽到男同学的概率大还是抽到女同学的概率大?
![]() 若老师已从盒子中抽出了
若老师已从盒子中抽出了![]() 张小卡片,其中有
张小卡片,其中有![]() 个是男同学,并把这
个是男同学,并把这![]() 张小卡片放在一边,再从盒子中抽出第
张小卡片放在一边,再从盒子中抽出第![]() 张小卡片,则这时女同学被抽到的概率是多少?
张小卡片,则这时女同学被抽到的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com