
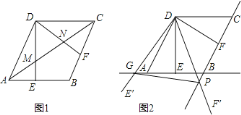
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.
![]() 如图
如图![]() ,连接
,连接![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,求证:
,求证:![]() ;
;
![]() 如图
如图![]() ,将
,将![]() 以点
以点![]() 为旋转中心旋转,其两边
为旋转中心旋转,其两边![]() 、
、![]() 分别与直线
分别与直线![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() ,连接
,连接![]() ,当
,当![]() 的面积等于
的面积等于![]() 时,求旋转角的大小并指明旋转方向.
时,求旋转角的大小并指明旋转方向.
科目:初中数学 来源: 题型:
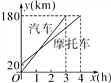
【题目】一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:①摩托车比汽车晚到1h;②A,B两地的路程为20km;③摩托车的速度为45km/h,汽车的速度为60km/h;④汽车出发1小时后与摩托车相遇,此时距B地40千米.其中正确结论的个数是( )
A. 2个 B. 3个 C. 4个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形![]() 的边长为
的边长为![]() ,
,![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 在坐标轴上,把正方形
在坐标轴上,把正方形![]() 绕点
绕点![]() 顺时针旋转后得到正方形
顺时针旋转后得到正方形![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,且点
,且点![]() 恰为
恰为![]() 的中点,则点
的中点,则点![]() 的坐标为________.
的坐标为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() ,
,![]() 是对角线
是对角线![]() 上一点,
上一点,![]() 是线段
是线段![]() 延长线上一点,且
延长线上一点,且![]() ,连接
,连接![]() 、
、![]() .
.
![]() 若
若![]() 是线段
是线段![]() 的中点,如图
的中点,如图![]() ,易证:
,易证:![]() (不需证明);
(不需证明);
![]() 若
若![]() 是线段
是线段![]() 或
或![]() 延长线上的任意一点,其它条件不变,如图
延长线上的任意一点,其它条件不变,如图![]() 、图
、图![]() ,线段
,线段![]() 、
、![]() 有怎样的数量关系,直接写出你的猜想;并选择一种情况给予证明.
有怎样的数量关系,直接写出你的猜想;并选择一种情况给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点 D,E 分别在边 AC,AB 上,BD 与 CE 交于点 O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.
(1)上述三个条件中,由哪两个条件可以判定△ABC 是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了看一种图钉落地后钉尖着地的概率有多大,小明作了![]() 次试验,其中钉尖着地的次数是
次试验,其中钉尖着地的次数是![]() 次.下列说法错误的是( )
次.下列说法错误的是( )
A. 钉尖着地的频率是![]()
B. 前![]() 次试验结束后,钉尖着地的次数一定是
次试验结束后,钉尖着地的次数一定是![]() 次
次
C. 钉尖着地的概率大约是![]()
D. 随着试验次数的增加,钉尖着地的频率稳定在![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校图书馆大楼工程在招标时,接到甲乙两个工程队的投标书,每施工一个月,需付甲工程队工程款16万元,付乙工程队12万元。工程领导小组根据甲乙两队的投标书测算,可有三种施工方案:
(1)甲队单独完成此项工程刚好如期完工;
(2)乙队单独完成此项工程要比规定工期多用3个月;
(3)若甲乙两队合作2个月,剩下的工程由乙队独做也正好如期完工。
你觉得哪一种施工方案最节省工程款,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数![]() ,则下列关于该函数的描述中,错误的是( )
,则下列关于该函数的描述中,错误的是( )
A. 该函数的最小值是![]()
B. 该函数图象与![]() 轴没有交点
轴没有交点
C. 该函数图象与![]() 轴有两个不同的交点
轴有两个不同的交点
D. 当![]() 时,
时,![]() 随着
随着![]() 的增大而增大
的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某场足球比赛中,球员甲从球门底部中心点![]() 的正前方
的正前方![]() 处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为
处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为![]() 时达到最高点,此时足球飞行的水平距离为
时达到最高点,此时足球飞行的水平距离为![]() .已知球门的横梁高
.已知球门的横梁高![]() 为
为![]() .
.

![]() 在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
![]() 守门员乙站在距离球门
守门员乙站在距离球门![]() 处,他跳起时手的最大摸高为
处,他跳起时手的最大摸高为![]() ,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com