
【题目】如图,![]() ,
,![]() ,点D在边BC上
,点D在边BC上![]() 与B、C不重合
与B、C不重合![]() ,四边形ADEF为正方形,过点F作
,四边形ADEF为正方形,过点F作![]() ,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:
,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:![]() ;
;![]() :
:![]() :2;
:2;![]() ;
;![]() ,其中正确的结论的个数是()
,其中正确的结论的个数是()

A.1B.2C.3D.4
【答案】D
【解析】
由正方形的性质得出∠FAD=90°,AD=AF=EF,证出∠CAD=∠AFG,由AAS证明△FGA≌△ACD,得出AC=FG,①正确;
证明四边形CBFG是矩形,得出S△FAB=![]() FBFG=
FBFG=![]() S四边形CBFG,②正确;
S四边形CBFG,②正确;
由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°,③正确;
证出△ACD∽△FEQ,得出对应边成比例,得出DFE=AD2=FQAC,④正确.
解:∵四边形ADEF为正方形,
∴∠FAD=90°,AD=AF=EF,
∴∠CAD+∠FAG=90°,
∵FG⊥CA,
∴∠GAF+∠AFG=90°,
∴∠CAD=∠AFG,
在△FGA和△ACD中,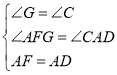
∴△FGA≌△ACD(AAS),
∴AC=FG,①正确;
∵BC=AC,
∴FG=BC,
∵∠ACB=90°,FG⊥CA,
∴FG∥BC,
∴四边形CBFG是矩形,
∴∠CBF=90°,S△FAB=![]() FBFG=
FBFG=![]() S四边形CBFG,②正确;
S四边形CBFG,②正确;
∵CA=CB,∠C=∠CBF=90°,
∴∠ABC=∠ABF=45°,③正确;
∵∠FQE=∠DQB=∠ADC,∠E=∠C=90°,
∴△ACD∽△FEQ,
∴AC:AD=FE:FQ,
∴ADFE=AD2=FQAC,④正确;
所以①②③④正确.
故选:D.


 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】有![]() 、
、![]() 两个不透明的布袋,
两个不透明的布袋,![]() 袋中有三个相同的小球,分别标有数字
袋中有三个相同的小球,分别标有数字![]() ,
,![]() 和
和![]() ,
,![]() 袋中有两个相同的小球,分别标有数字
袋中有两个相同的小球,分别标有数字![]() 和
和![]() ,小林从
,小林从![]() 袋中随机取出一个小球,记录标有的数字为
袋中随机取出一个小球,记录标有的数字为![]() ,再从
,再从![]() 袋中随机取出一个小球,记录标有的数字为
袋中随机取出一个小球,记录标有的数字为![]() ,这样确定了点
,这样确定了点![]() 的坐标
的坐标![]()
![]() 用画树状图或列表的形式,求点
用画树状图或列表的形式,求点![]() 在
在![]() 轴上的概率;
轴上的概率;
![]() 在平面直角坐标系
在平面直角坐标系![]() 中,
中,![]() 的半径是
的半径是![]() ,求过点
,求过点![]() 能作
能作![]() 切线的概率.
切线的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,![]() 垂直
垂直![]() ,AB=6,Δ
,AB=6,Δ![]() 是等边三角形,点
是等边三角形,点![]() 在射线
在射线![]() 上运动,以
上运动,以![]() 为边向右上方作等边Δ
为边向右上方作等边Δ![]() ,射线
,射线![]() 与射线
与射线![]() 交于点
交于点![]() .
.
(1)如图1,当点![]() 运动到与点
运动到与点![]() 成一条直线时,
成一条直线时,![]() (填长度),∠
(填长度),∠![]() 度.
度.

(2)在图2中,①求证:∠![]() ;
;
②随着点![]() 的运动,∠
的运动,∠![]() 的度数是否发生改变?若不变,求出这个角的度数;若改变,说明理由.
的度数是否发生改变?若不变,求出这个角的度数;若改变,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2017年张学友演唱会”于6月3日在我市关山湖奥体中心举办,小张去离家2520米的奥体中心看演唱会,到奥体中心后,发现演唱会门票忘带了,此时离演唱会开始还有23分钟,于是他跑步回家,拿到票后立刻找到一辆“共享单车”原路赶回奥体中心,已知小张骑车的时间比跑步的时间少用了4分钟,且骑车的平均速度是跑步的平均速度的1.5倍.
(1)求小张跑步的平均速度;
(2)如果小张在家取票和寻找“共享单车”共用了5分钟,他能否在演唱会开始前赶到奥体中心?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个如图所示的面积为300![]() 的长方形围栏,围栏总长50m,一边靠墙(墙长25m),
的长方形围栏,围栏总长50m,一边靠墙(墙长25m),

(1)求围栏的长和宽;
(2)能否围成面积为400 ![]() 的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位需采购一批商品,购买甲商品10件和乙商品15件需资金350元,而购买甲商品15件和乙商品10件需要资金375元.
![]() 求甲、乙商品每件各多少元?
求甲、乙商品每件各多少元?
![]() 本次计划采购甲、乙商品共30件,计划资金不超过460元,
本次计划采购甲、乙商品共30件,计划资金不超过460元,
![]() 最多可采购甲商品多少件?
最多可采购甲商品多少件?
![]() 若要求购买乙商品的数量不超过甲商品数量的
若要求购买乙商品的数量不超过甲商品数量的![]() ,请给出所有购买方案,并求出该单位购买这批商品最少要用多少资金.
,请给出所有购买方案,并求出该单位购买这批商品最少要用多少资金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+2分别与x轴、y轴相交于点A、点B
x+2分别与x轴、y轴相交于点A、点B

(1)求点A和点B的坐标;
(2)若点P是y轴上的一点,设△AOB、△ABP的面积分别为S△AOB与S△ABP,且S△ABP=2S△AOB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
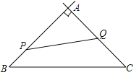
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,现有动点
,现有动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向运动,动点
方向运动,动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向运动,已知点
方向运动,已知点![]() 的速度是
的速度是![]() ,点
,点![]() 的速度是
的速度是![]() ,它们同时出发,经过________秒,
,它们同时出发,经过________秒,![]() 的面积是
的面积是![]() 面积的一半?
面积的一半?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com