Question

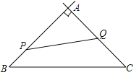
【题目】如图，∠AOB=30°，点P位于∠AOB内，OP=3，点M，N分别是射线OA、OB边上的动点，当△PMN的周长最小时，则∠MPN的度数为__________°.

Answer 1

【答案】120

【解析】

要求∠NPM的度数，要在△NPM中进行，根据轴对称的性质和等腰三角形的性质可证∠CPN=∠C，∠DPM=∠D，然后证明∠C+∠D=∠AOB,利用四边形内角和可得答案．

解：作P关于OB、OA的对称点C、D，连接CD交OB、OA于N、M．

此时△PNM周长有最小值；

∵P关于OB、OA的对称点C、D，，

∴OB垂直平分PC，OA垂直平分PD，

∴CN=PN，PM=DM，

∴∠CPN=∠C，∠DPM=∠D，

∵∠PRN=∠PTM=90°，

∴∠ONM=∠BNC=90-∠C, ∠OMN=∠BMD=90°-∠D,

∵∠ONM+∠OMN+∠AOB=180°,

∴90-∠C+90°-∠D+∠AOB=180°,

∴∠C+∠D=∠AOB,

∴∠CPN+∠DPM=∠AOB=30°，

在四边形OTPR中，

∴∠CPD+∠BOA=180°，

∵∠NPM+∠CPN+∠DPM+∠AOB =180°，

∴∠NPM=180°-30°-30°∠=120°.

故答案为120．