
 某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元.为按时完成任务,该企业招收了新工人.设新工人李明第X天生产的粽子数量为y只,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$
某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元.为按时完成任务,该企业招收了新工人.设新工人李明第X天生产的粽子数量为y只,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$分析 (1)把y=420代入y=30x+120,解方程即可求得;
(2)根据图象求得成本p与x之间的关系,然后根据利润等于订购价减去成本价,然后整理即可得到W与x的关系式,再根据一次函数的增减性和二次函数的增减性解答;
解答 解:(1)设李明第n天生产的粽子数量为420只,
由题意可知:30n+120=420,
解得n=10.
答:第10天生产的粽子数量为420只.
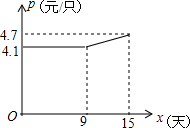
(2)由图象得,当0≤x<9时,p=4.1;
当9≤x≤15时,设P=kx+b,
把点(9,4.1),(15,4.7)代入得,$\left\{\begin{array}{l}{9k+b=4.1}\\{15k+b=4.7}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=0.1}\\{b=3.2}\end{array}\right.$,
∴p=0.1x+3.2,
①0≤x≤5时,w=(6-4.1)×54x=102.6x,当x=5时,w最大=513(元);
②5<x≤9时,w=(6-4.1)×(30x+120)=57x+228,
∵x是整数,
∴当x=9时,w最大=741(元);
③9<x≤15时,w=(6-0.1x-3.2)×(30x+120)=-3x2+72x+336,
∵a=-3<0,
∴当x=-$\frac{b}{2a}$=12时,w最大=768(元);
综上,当x=12时,w有最大值,最大值为768.
点评 本题考查的是二次函数在实际生活中的应用,主要是利用二次函数的增减性求最值问题,利用一次函数的增减性求最值,难点在于读懂题目信息,列出相关的函数关系式.


科目:初中数学 来源: 题型:解答题
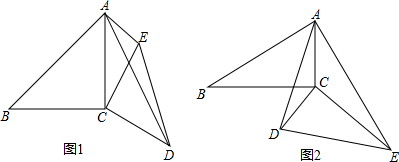
 已知:如图,点B(3,3)在双曲线y=$\frac{k}{x}$(其中x>0)上,点D在双曲线y=$\frac{-4}{x}$ (其中x<0)上,点A、C分别在x、y轴的正半轴上,且点A、B、C、D围成的四边形为正方形.
已知:如图,点B(3,3)在双曲线y=$\frac{k}{x}$(其中x>0)上,点D在双曲线y=$\frac{-4}{x}$ (其中x<0)上,点A、C分别在x、y轴的正半轴上,且点A、B、C、D围成的四边形为正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
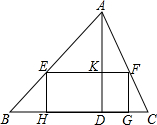 已知锐角△ABC中,边BC长为12,高AD长为8.
已知锐角△ABC中,边BC长为12,高AD长为8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
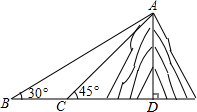 如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为137米(结果保留整数,测角仪忽略不计,$\sqrt{2}$≈1.414,$\sqrt{3}$,1.732)
如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为137米(结果保留整数,测角仪忽略不计,$\sqrt{2}$≈1.414,$\sqrt{3}$,1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com